拓扑图作为现代数学中的一个核心概念,不仅在纯粹的数学研究中占据着重要地位,也在计算机科学、物理学、经济学等多个领域产生了深远的影响。尤其是图论领域,拓扑图的研究不仅深化了人们对图的结构和性质的理解,还开辟了许多新的研究方向。在本文中,我们将带您一探拓扑图的神秘面纱,探索它的基础理论以及它在各个学科中的广泛应用。
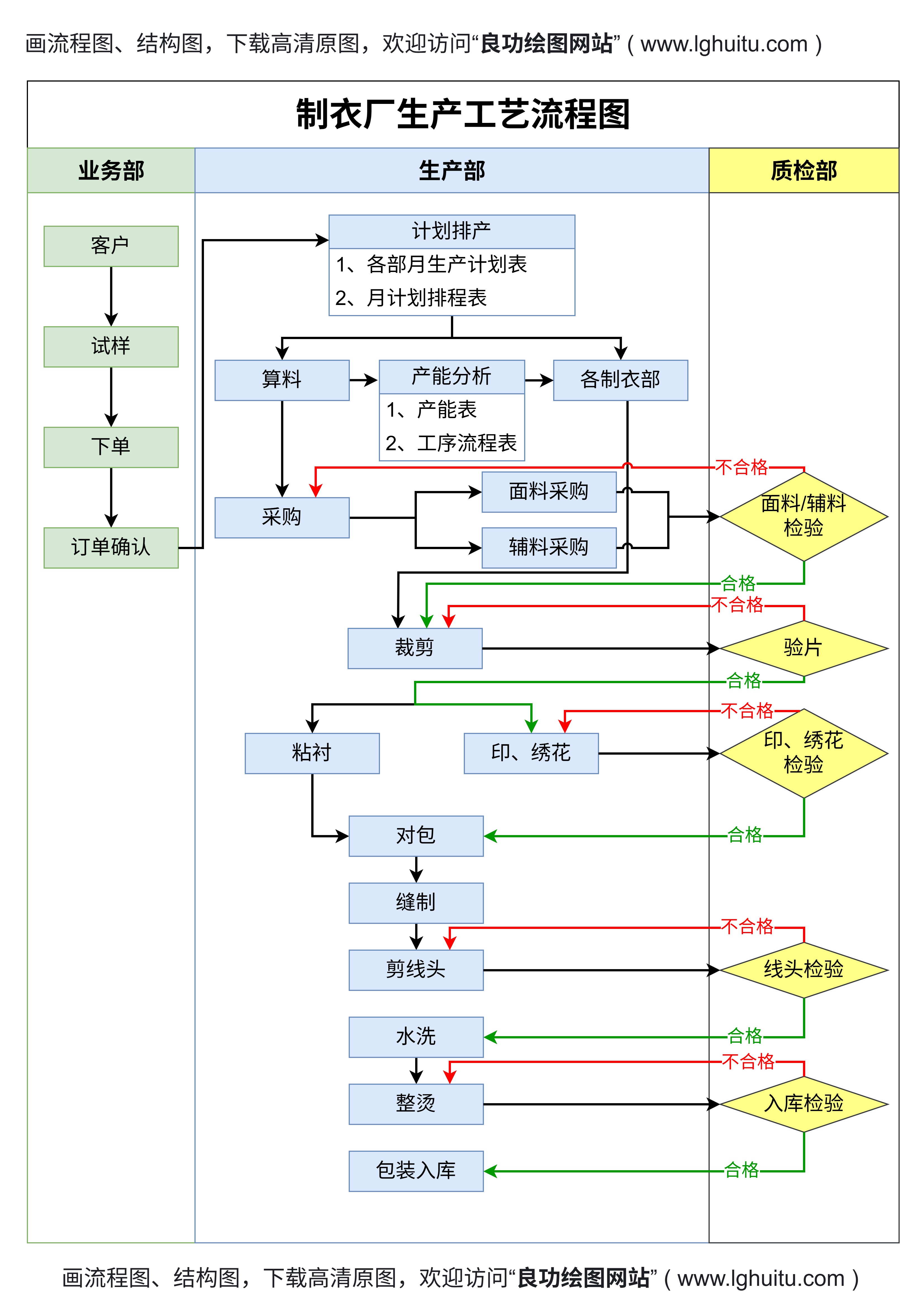
拓扑学是研究空间性质与形状不变性的数学分支,它研究的对象是一些“形状”或“空间”,这些空间在某些变换下不会发生显著变化。而拓扑图,正是通过图形的形式将这些空间的特征和属性展示出来。拓扑图的关键在于“不改变连接关系”。简单来说,拓扑图强调的是图中节点和节点之间的连接方式,而非节点的实际位置或图形的具体形状。举个例子,如果我们把一个圆形变形为一个椭圆形,只要节点的连接关系没有改变,这两者在拓扑学中是等价的。
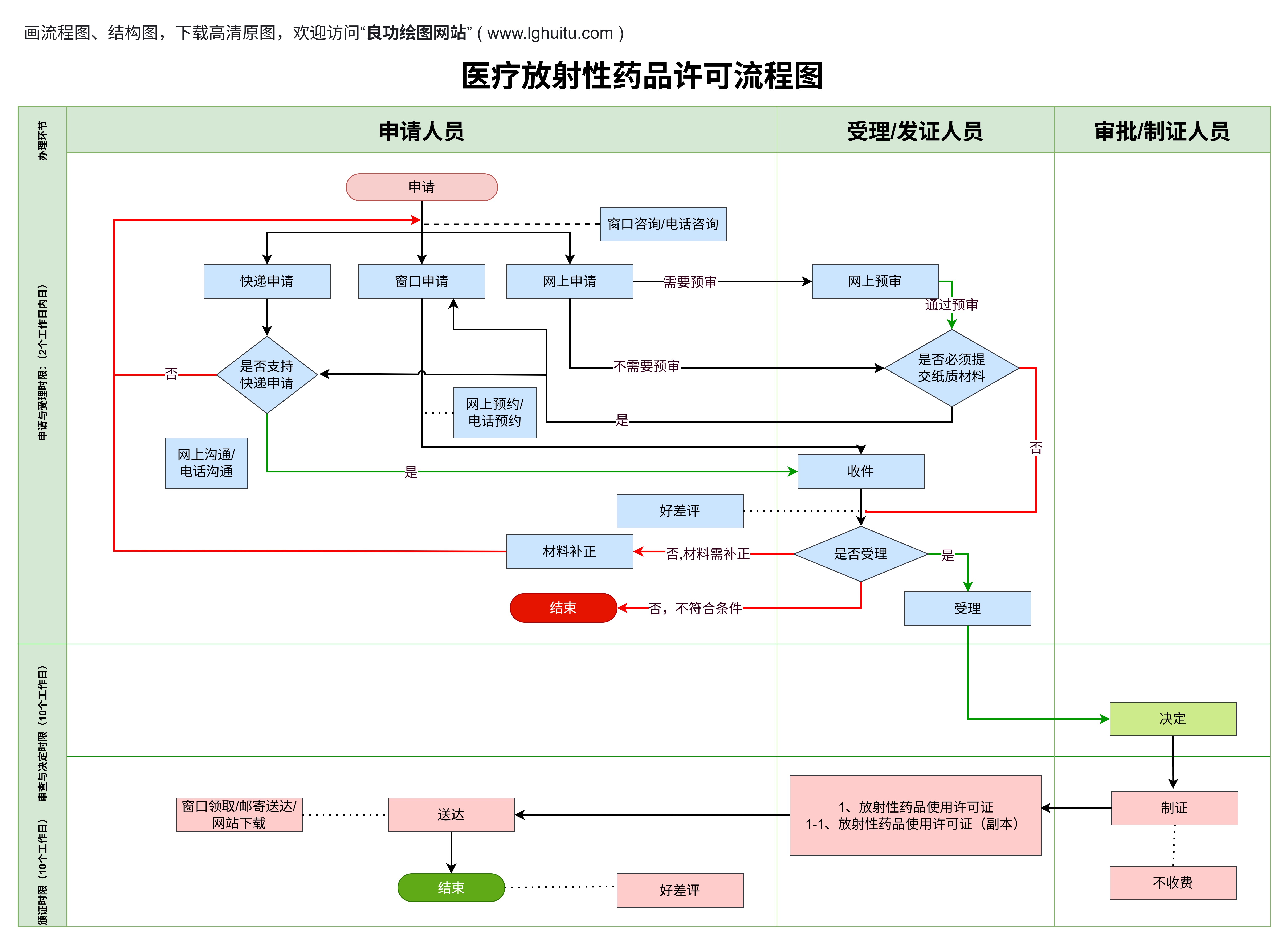
拓扑图常常用于表示某一系统中的元素及其相互关系。在图论中,我们将图中的每个点视为系统的一个节点,而每条边则代表了节点间的某种联系。比如,在社交网络中,每个人可以看作一个节点,人与人之间的友谊关系就是边。而在拓扑图的框架下,我们更多地关注的是这些关系如何通过不同的路径和结构相互交织。
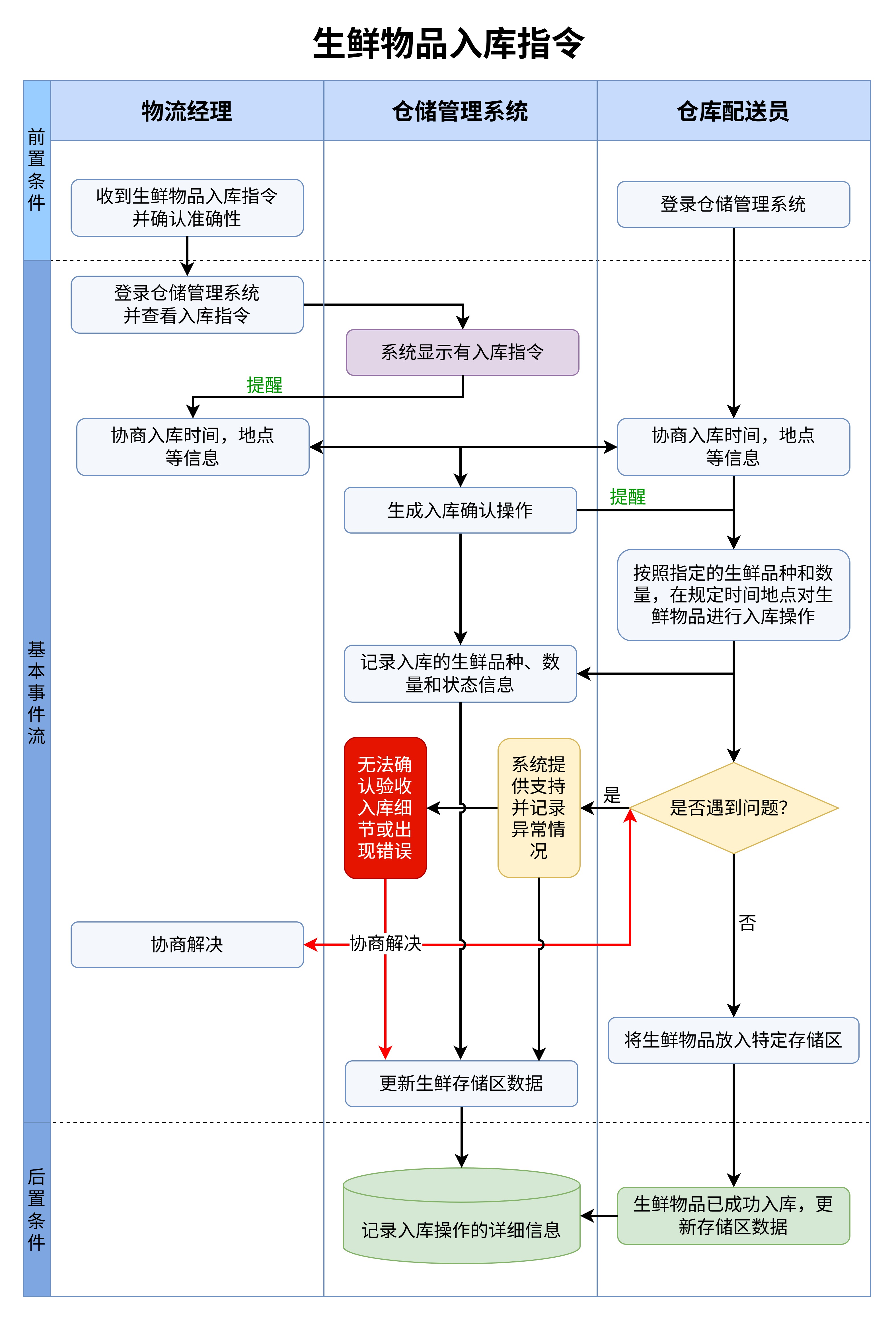
拓扑图在计算机科学中有着广泛的应用,特别是在计算机网络的设计与优化中。计算机网络的拓扑结构决定了信息流动的效率与稳定性。例如,网络的拓扑结构可以是星型、环型、总线型或树型等,每种结构在传输速度、容错能力、易扩展性等方面都有不同的表现。而拓扑图的作用就是帮助网络工程师通过图形化的方式了解这些结构的优缺点,从而设计出更高效的网络布局。
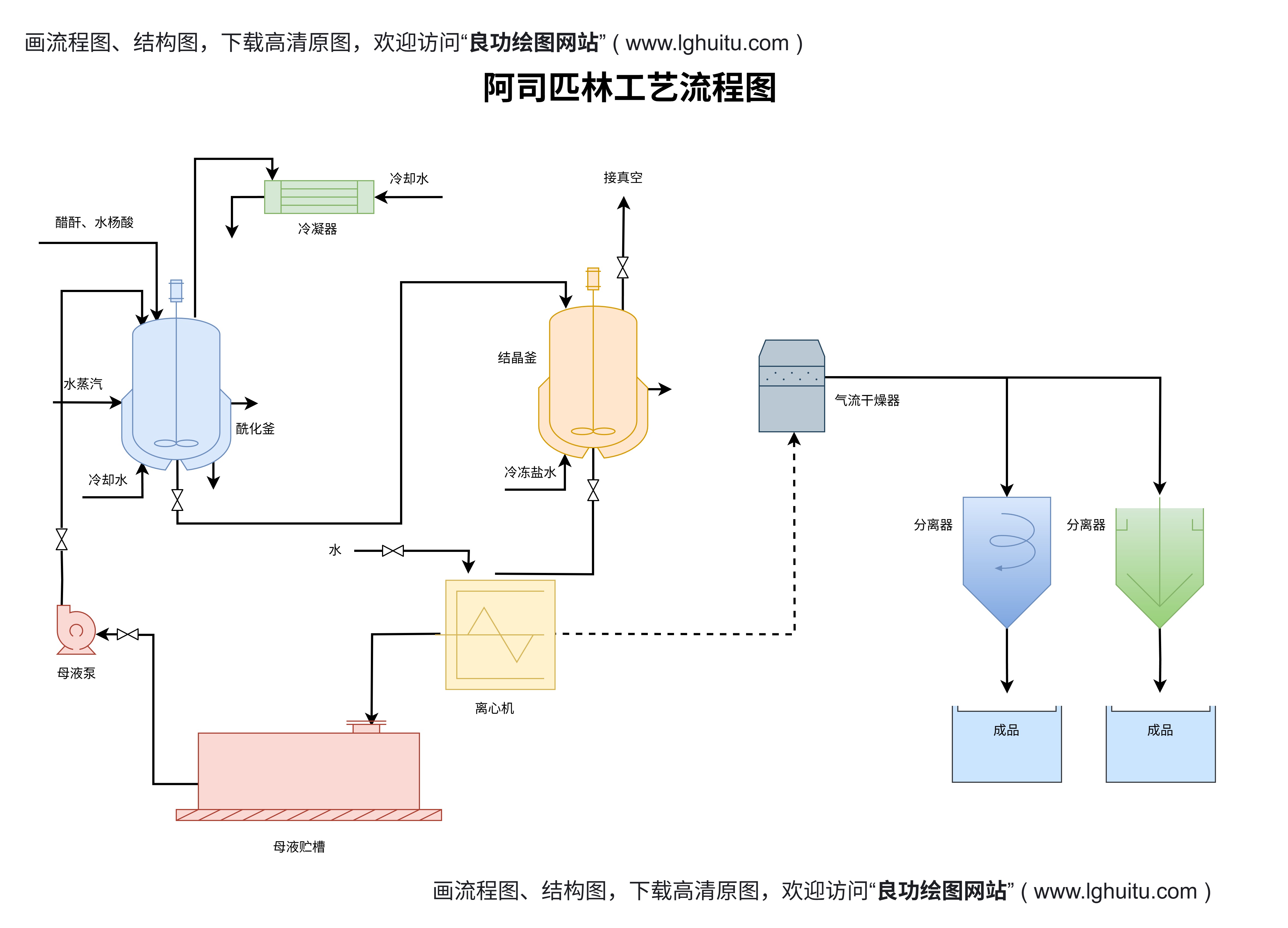
在大规模的互联网应用中,拓扑图也起到了至关重要的作用。通过分析网络中的节点和连接关系,能够有效地发现潜在的瓶颈,预测可能的故障点,并根据需求进行相应的优化。例如,云计算平台中的分布式系统,往往需要通过拓扑图来展示各个节点之间的关系和负载情况,以保证资源的合理调配和系统的高效运行。
拓扑图还在数据流、通信协议、路由算法等领域发挥着重要作用。例如,路由协议中的“最短路径问题”就是一个典型的图论问题。通过拓扑图,网络设备可以计算出最短的传输路径,确保信息能够以最低的延迟和最低的成本到达目的地。

拓扑图不仅仅局限于计算机网络领域,它在物理学中也有着广泛的应用。在量子力学和粒子物理学中,拓扑学提供了一种分析复杂系统的新方法。拓扑量子场论就是一种通过拓扑学方法研究量子物理的理论,它为物理学家理解粒子相互作用提供了新的视角。
以量子计算为例,量子计算机的计算结构本质上是由大量量子比特(qubit)组成的量子网络。这些量子比特之间的纠缠关系和计算过程的路径可以通过拓扑图进行建模。通过这些拓扑图,研究人员可以预测量子计算过程中可能出现的错误和问题,并采取相应的修正措施,提升计算精度和效率。
拓扑学还在流体力学和天体物理学中有着显著的应用。在研究气流和水流的流动模式时,拓扑学帮助研究人员揭示了这些复杂现象背后的数学规律。同样,在研究天体的结构和宇宙中的物质分布时,拓扑学也提供了一种重要的工具,用以分析和描述空间的性质。
拓扑图的应用并不仅限于传统的自然科学,它还在社会科学,尤其是经济学中发挥着越来越重要的作用。在经济学中,拓扑图被用来分析市场中的供需关系、产业链的结构以及市场竞争格局等方面。例如,在分析全球供应链时,拓扑图可以帮助研究者更好地理解各个国家和地区之间的经济联系和相互依存关系。通过这些拓扑图,决策者可以识别出关键节点,预测某些市场的波动可能对其他区域产生的影响。
拓扑图还在博弈论中发挥着关键作用。博弈论研究的是各个决策者在特定规则下的策略选择,而拓扑图则可以帮助展示不同决策者之间的互动关系。在多方博弈中,拓扑图有助于识别可能的均衡点,帮助分析市场中的竞争与合作机制。它为经济学家提供了一个更加系统化、结构化的思考框架,使得复杂的市场行为得以简化和可视化。
近年来,拓扑图在人工智能领域的应用越来越受到关注。人工智能的发展,尤其是在深度学习和神经网络领域,依赖于大量的数据和复杂的网络结构。拓扑图能够有效地帮助人工智能系统理解数据之间的内在联系。在图神经网络(GNN)中,拓扑图被用来构建图结构,从而使神经网络能够对图中的节点和边进行学习与推理。通过这种方式,人工智能可以在不规则的数据结构中进行有效的分类、预测和推荐。
拓扑图还在图像处理、自然语言处理等领域中得到了广泛应用。例如,在图像识别中,拓扑学被用来提取图像中的形状特征,从而帮助计算机更好地理解和分类图像内容。在自然语言处理领域,拓扑图也可以帮助理解语句之间的关系,提升机器翻译和语义理解的能力。
随着科学技术的不断发展,拓扑图的应用领域也在不断扩展。无论是在网络技术、物理学,还是在经济学和人工智能领域,拓扑图都以其独特的方式发挥着越来越重要的作用。可以预见,在未来的技术革命中,拓扑图将继续为我们揭示更多复杂系统背后的内在规律,为各行各业提供更加高效的解决方案。
拓扑图不仅仅是数学中的一个抽象工具,它已经成为我们理解和处理复杂系统的一个桥梁。无论是在实际应用中,还是在理论研究上,拓扑图都将继续拓展我们的认知边界,引领我们走向更加智能和高效的未来。