拓扑图,作为数学领域中一种富有魅力的图形结构,虽然源自于复杂的抽象理论,但它在现代科技中却扮演着至关重要的角色。从数据传输、网络设计,到物理学、社会学等领域,拓扑图为我们提供了一种理解复杂系统之间联系的有力工具。什么是拓扑图,它为什么如此重要呢?
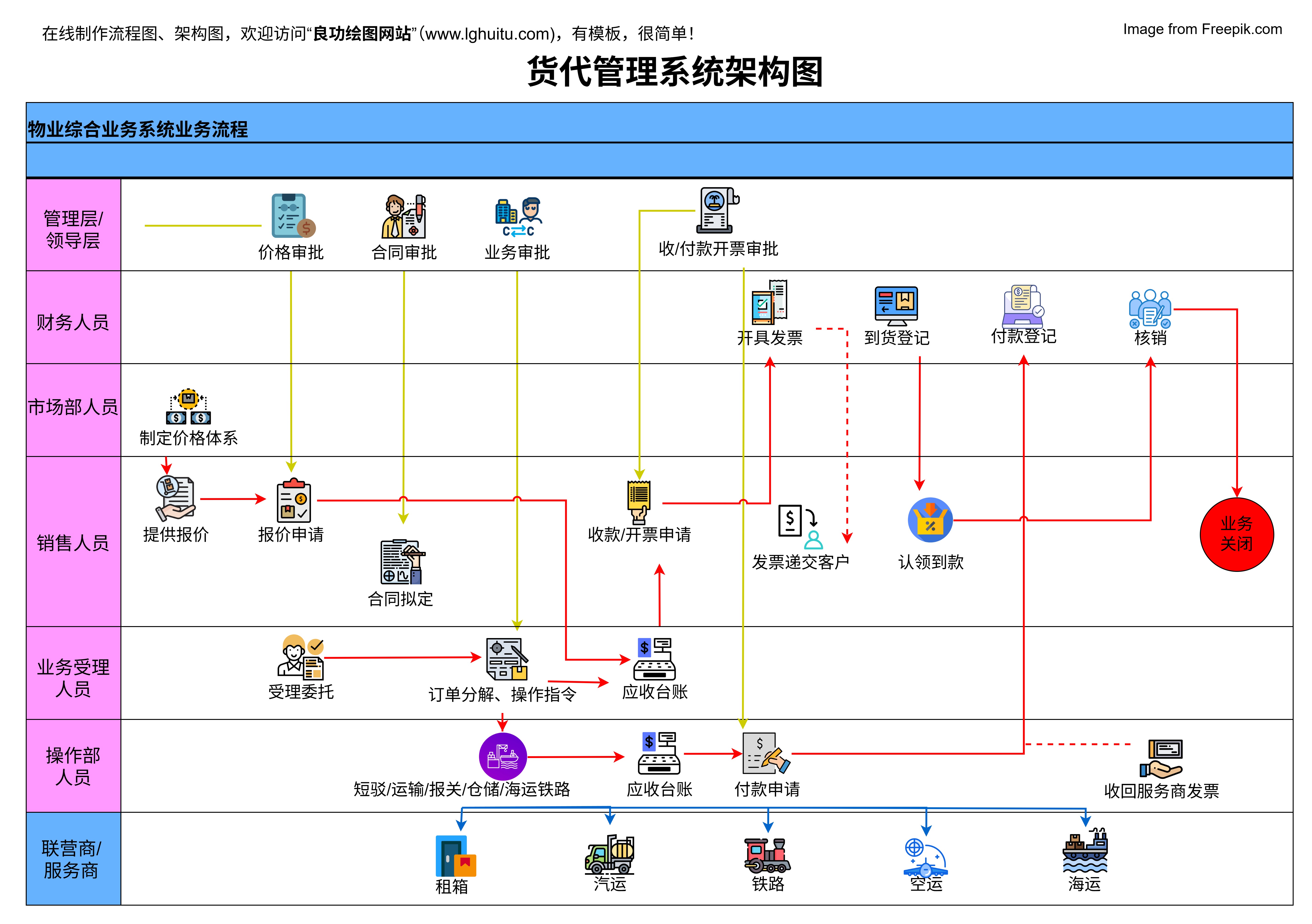
拓扑图,又称拓扑结构图,最初来源于拓扑学这一数学分支。简单来说,拓扑学研究的是空间在连续变形下保持不变的性质,而拓扑图则是对物体之间连接关系的一种抽象表示。在拓扑图中,节点代表系统中的对象,边则代表这些对象之间的连接或关系。
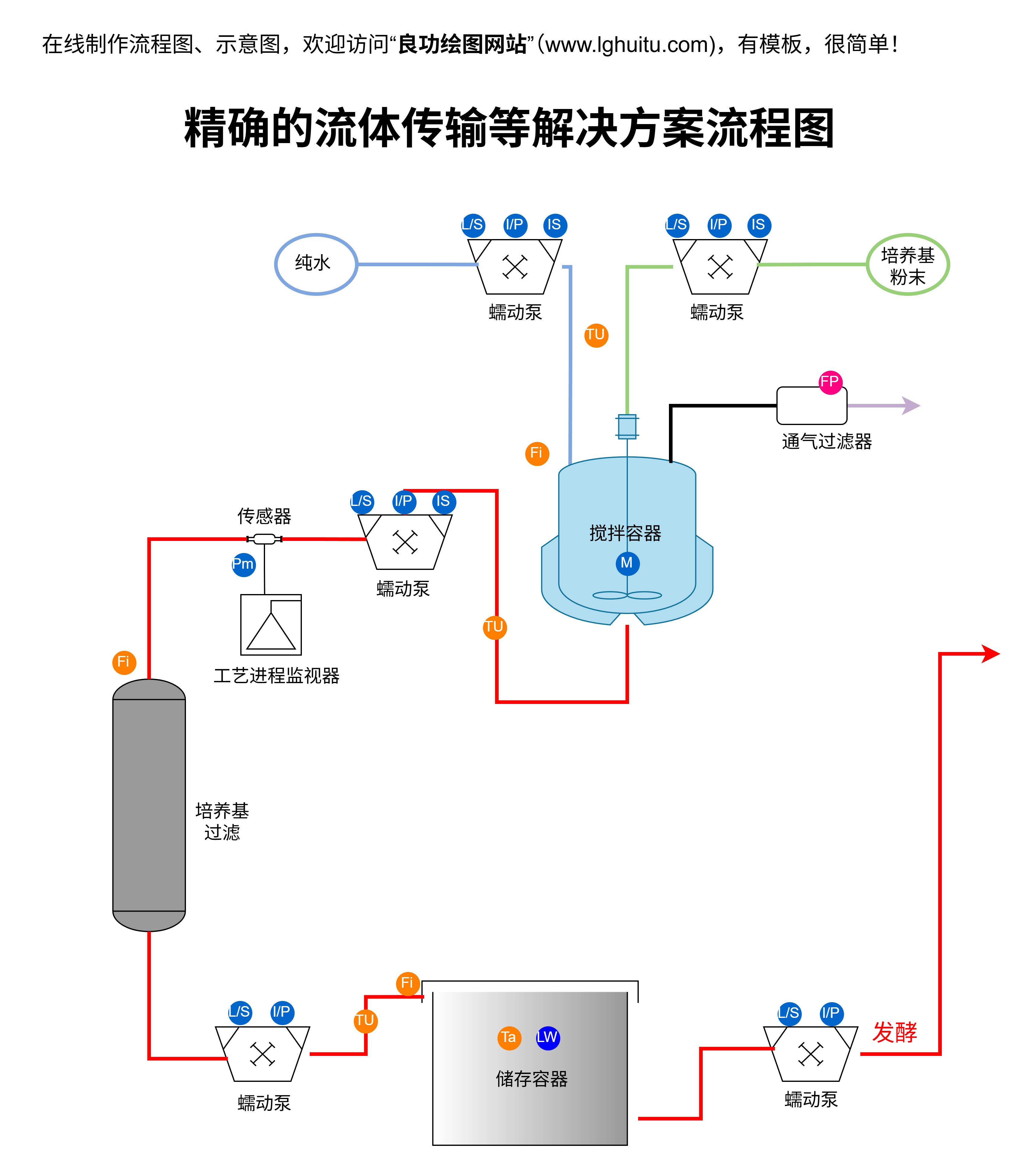
与普通的图形结构不同,拓扑图更关注的是“关系”而非具体的“形状”。例如,在拓扑学中,一个圆和一个方形被认为是相同的,因为它们的本质属性(连通性)没有改变,尽管它们的形状不同。这种灵活的视角使拓扑图在多个学科中都得到了广泛的应用。
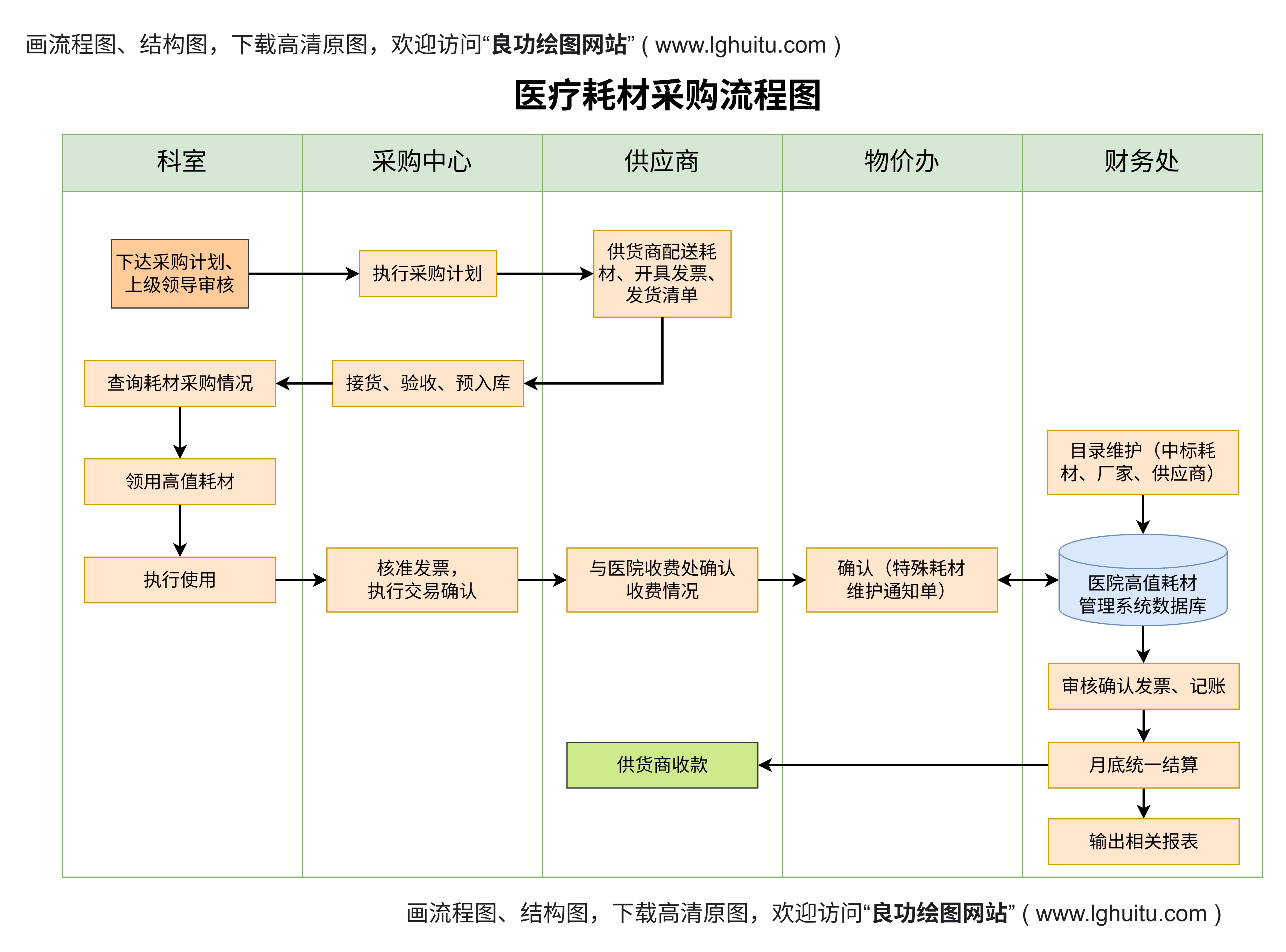
拓扑图的魅力在于它能够捕捉复杂系统中的关系和连接性,尤其适用于描述那些无法通过传统几何方式表达的网络结构。它的基本特性包括:
节点和边:拓扑图由节点(点)和边(连接节点的线)构成。节点代表系统中的实体,边代表实体之间的联系。
连通性:拓扑图的一个关键概念是连通性,指的是在图中是否可以通过边从一个节点到达另一个节点。如果一个图中的任意两个节点都有路径连接,那么该图被称为“连通”的。
无向与有向:拓扑图可以分为无向图和有向图。无向图中的边没有方向,表示节点之间是相互连接的;而有向图中的边是有方向的,表示节点之间的连接具有单向性。
图的平面性与拓扑变换:拓扑图不仅仅关注图的“平面”呈现,它还允许图形在不改变连通性的前提下进行变形。这种特性对于很多实际问题的建模至关重要。
拓扑图并非仅限于理论研究,它在许多实际应用中也得到了广泛的运用。我们来看看它在各个领域中的实际价值:
计算机网络与通信:在计算机网络中,拓扑图常常用来描述网络设备(如路由器、交换机、服务器等)之间的连接关系。通过研究网络拓扑结构,可以优化数据传输路径,提高网络的效率和稳定性。网络拓扑不仅有助于监控网络运行,还能预测和排查网络故障。
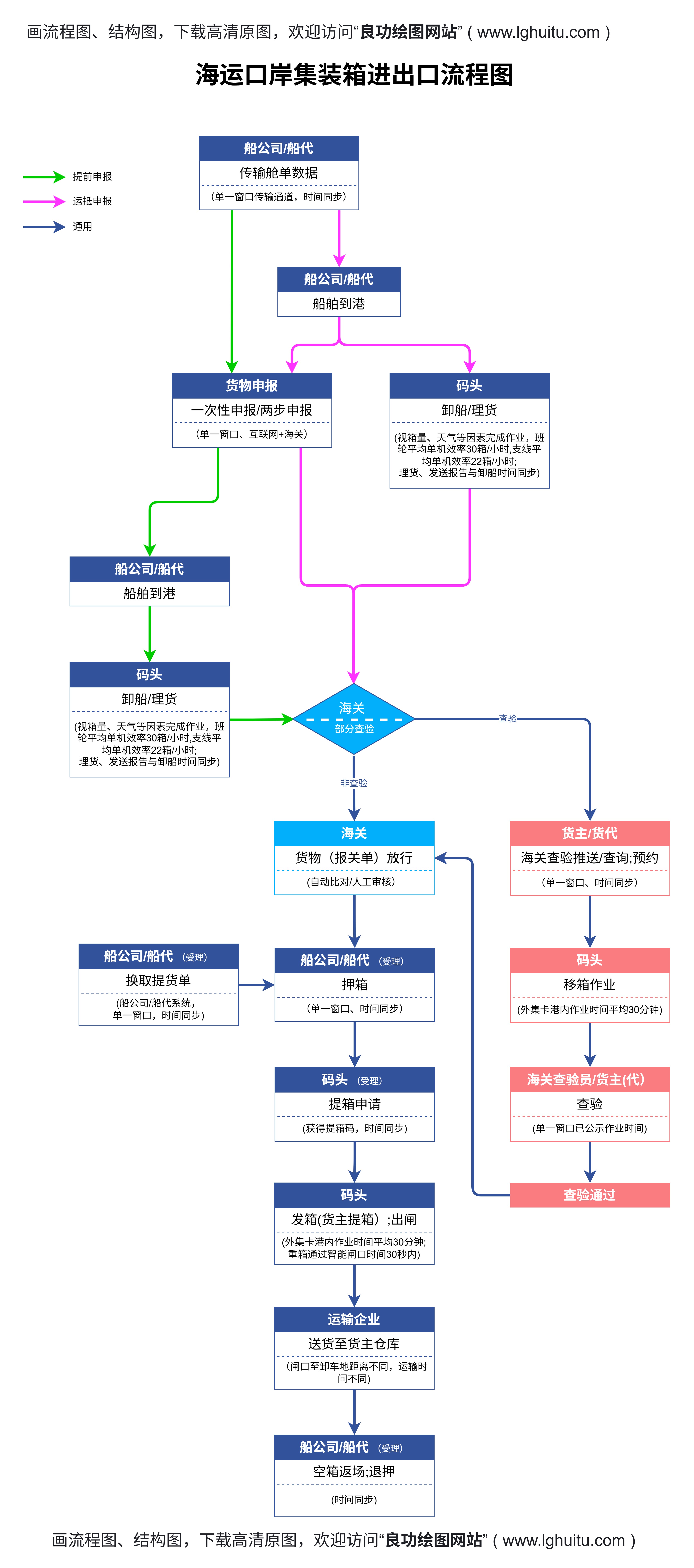
社交网络分析:在社交网络中,每个人可以视为一个节点,人与人之间的关系则通过边连接。社交网络中的信息传播、社区划分、影响力分析等都可以通过拓扑图来实现。通过拓扑分析,能够识别社交网络中的核心节点、群体结构以及信息流动模式。
生物学和生态学:在生物学中,拓扑图被用来描述物种之间的关系,尤其是在食物链、基因网络、生态系统中的相互关系。通过构建生物学拓扑图,科学家可以更好地理解生态系统的结构及其变化。
电力系统与交通网络:电力系统和交通网络的设计与优化同样依赖拓扑图。电力网中的电站、变电站、输电线路等构成了一个庞大的网络,拓扑图可以帮助工程师规划更为高效、稳定的电力传输路径。而在交通系统中,拓扑图帮助分析城市道路、公共交通线路等的连接性,优化交通流量,降低拥堵现象。
拓扑图的最大优势在于它能够将抽象的数学理论与现实世界中的复杂系统连接起来。它提供了一种从不同角度观察和分析系统结构的方式,不仅帮助我们发现系统内部的规律和模式,还能揭示出隐藏在这些复杂联系背后的深层次问题。
例如,互联网的拓扑结构不仅关乎信息的传输效率,更直接影响到网络安全和抗干扰能力。电力网的拓扑结构关系到电力的供应稳定性,而交通网络的拓扑结构直接影响到人们的出行效率。
拓扑图之所以在这些领域中大放异彩,正是因为它能够处理更高层次的关系和复杂性。在这背后,拓扑图所具备的数学理论支撑为其应用提供了坚实的基础,且随着科技的不断进步,它的潜力仍然远未被完全挖掘。
在大数据分析中,拓扑图成为了挖掘数据关系、预测趋势和模式识别的重要工具。比如,在电子商务、金融领域,通过构建用户行为的拓扑图,能够揭示消费者之间的行为模式,从而为精准营销、风险控制等提供决策支持。拓扑图能够帮助分析哪些节点(例如顾客、商品)是关键的,进而推动业务发展。
社交图谱分析:在社交媒体中,用户之间的关系构成了一个巨大的拓扑网络,通过分析这个社交图谱,可以洞察用户的兴趣爱好、行为习惯及其潜在的需求。例如,利用社交图谱,企业可以发现潜在的品牌推广者、意见领袖以及最具影响力的社交群体。
推荐系统优化:现代的推荐系统往往采用拓扑图结构来分析用户与商品、服务之间的关系。通过分析拓扑图,系统能够更好地预测用户的兴趣,从而提高推荐的精准度和满意度。这一应用不仅仅局限于电商平台,社交媒体、在线视频平台等也在广泛使用此技术来提升用户体验。

随着人工智能、物联网、量子计算等前沿技术的发展,拓扑图的作用愈加凸显。在未来的科技世界中,拓扑图将成为解决复杂问题的重要工具。
量子计算:量子计算依赖于量子态之间的复杂相互作用,这种相互作用可以通过拓扑学进行建模和分析。拓扑量子计算是量子计算领域的一项重要研究方向,利用拓扑学的概念来保证计算的稳定性和可靠性。
物联网:物联网中的设备数量巨大且分布广泛,拓扑图可以帮助设计更为高效的通信协议和网络架构,使设备之间的连接更加稳定和高效。在物联网的日常应用中,拓扑图同样可以优化资源分配和故障排查。
拓扑图作为一种深奥却实用的数学工具,不仅帮助我们在理论中理解复杂的系统结构,还推动了众多实际应用的发展。从计算机网络到社交媒体,从生物学到交通网络,拓扑图正在成为链接现实与理论之间的桥梁。随着技术的不断发展,拓扑图的应用场景将愈加广泛,成为我们探索和理解世界的重要工具。
拓扑图的神奇魅力,不仅仅是它的抽象性和深奥性,更在于它为我们揭示了世界万象之间的内在联系。