流体力学作为研究流体(如气体、液体)运动及其行为的学科,对于现代工业和工程应用有着至关重要的作用。在流体力学的众多概念中,流量(Q)和压差(△p)的关系尤为重要。无论是在管道输送、气流控制,还是在泵和风机的设计中,流量与压差的关系都扮演着关键的角色。今天,我们将深入分析这一关系,揭示它如何影响实际应用。
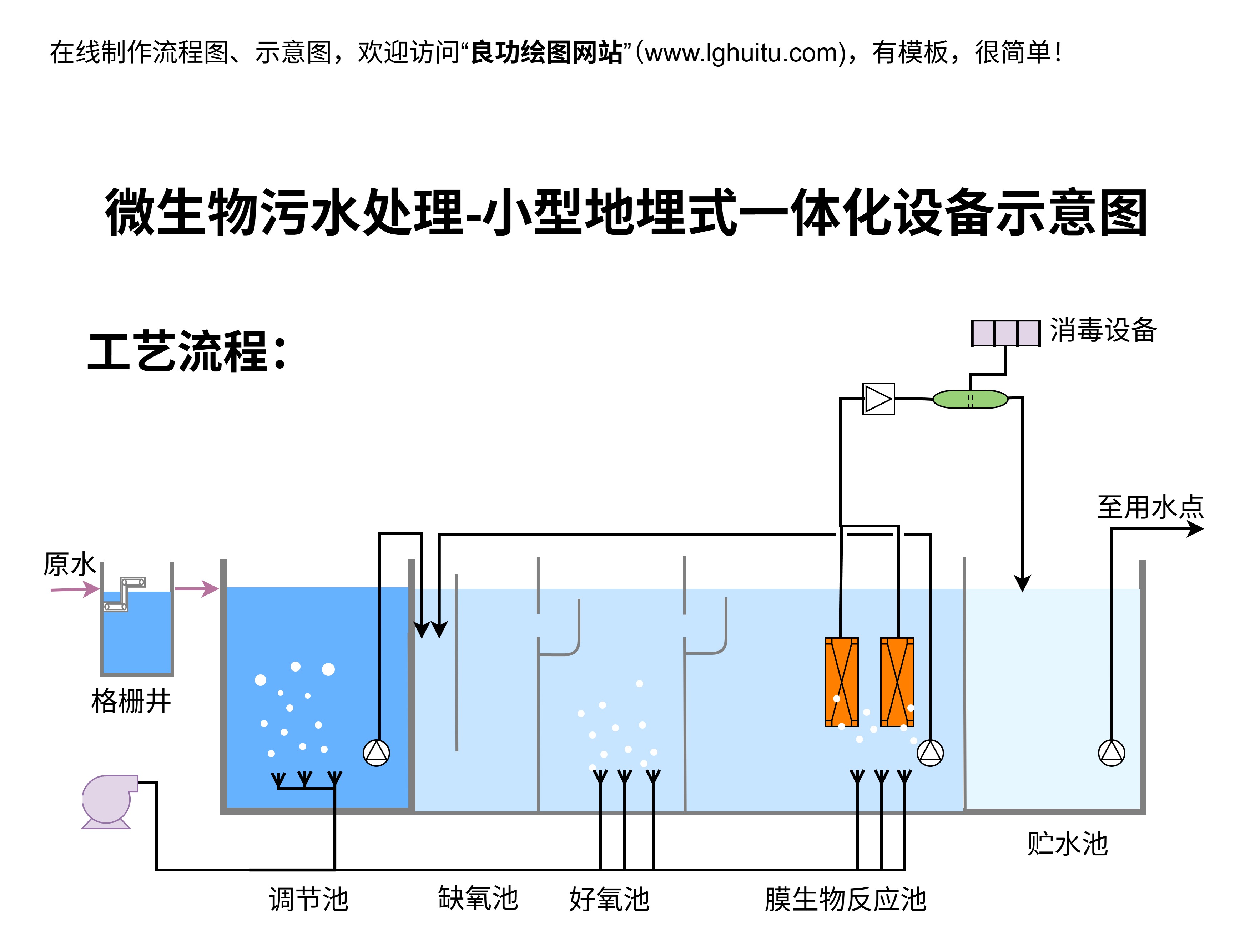
在流体力学中,流量Q通常指单位时间内通过管道或通道的流体体积或质量。常见的单位包括立方米每秒(m³/s)和升每分钟(L/min)。压差△p则是流体在管道中流动时,由于流体流动产生的压力差。简而言之,△p是两点之间流体压力的差异,它直接影响流体的流动能力。
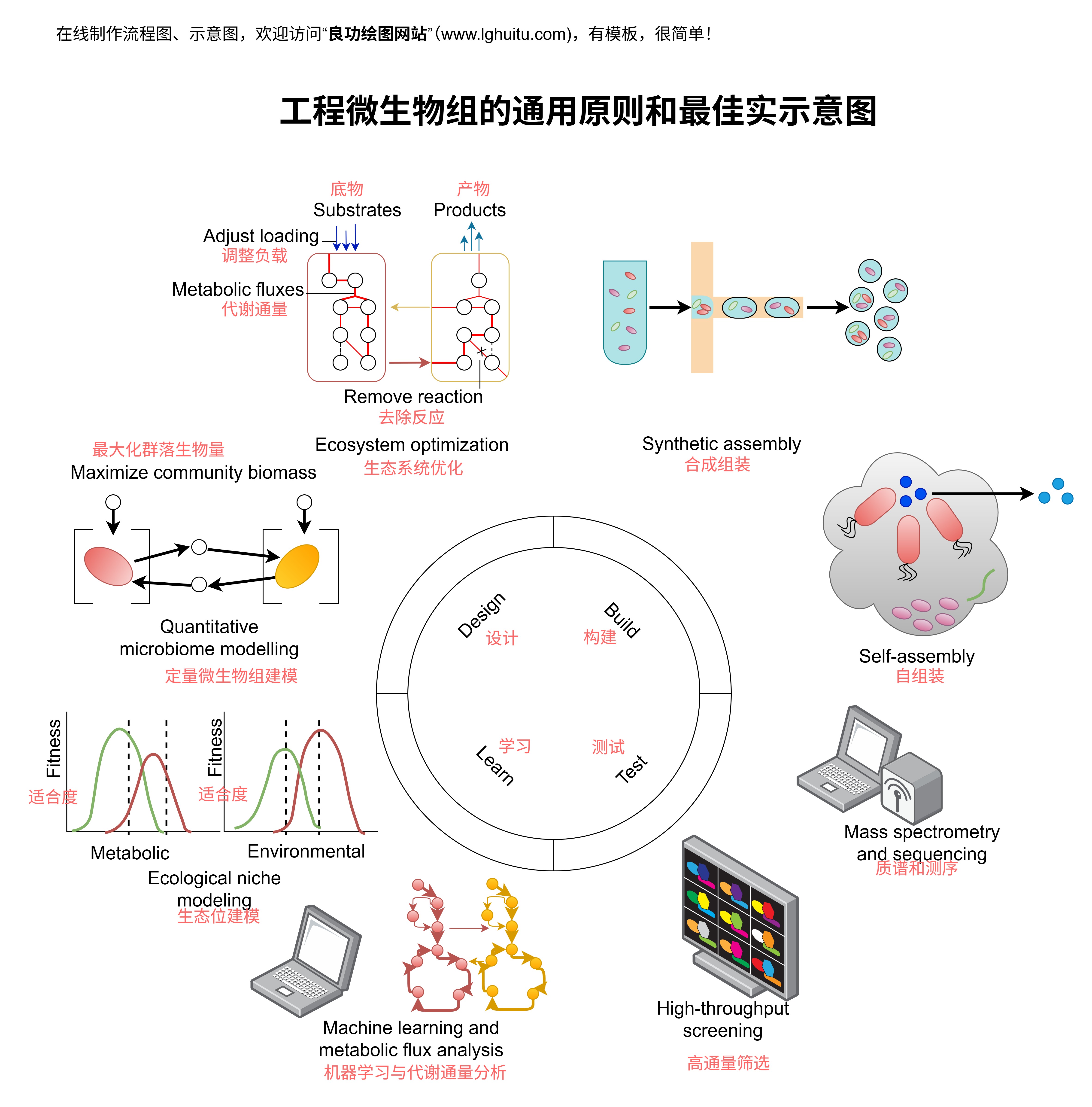
流体在管道中流动时,流量和压差之间有着密切的关系。流量越大,意味着单位时间内流体的体积或质量越多,压差通常也会增大。反之,流量减少时,压差也会减小。这个关系可以通过流体力学中的“伯努利方程”和“达西-魏斯巴赫方程”来解释。
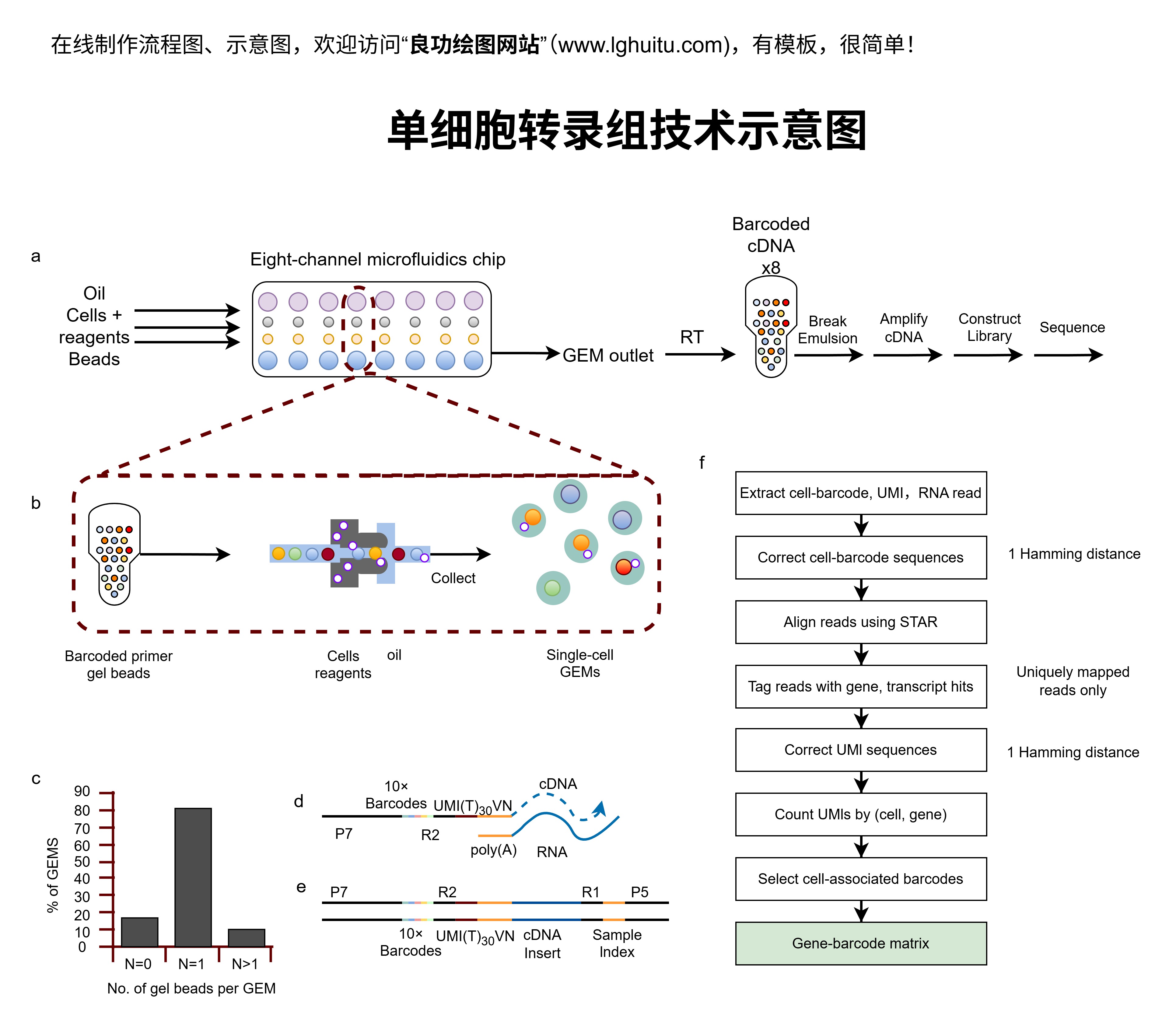
伯努利方程表明,在理想流体的情况下,流体的速度和压力存在相互转换的关系。对于实际流体(如水、空气等),流动的压差和流速、流量之间的关系则更加复杂,需要考虑摩擦力、流体的粘度等因素。
在很多工业管道系统中,流体的流动并非是理想状态,流动过程中会受到管道内摩擦力的影响。为了描述这种现象,达西-魏斯巴赫方程应运而生。该方程通过计算管道的摩擦损失,揭示了流量、压差、管道长度、直径和流体性质之间的关系。
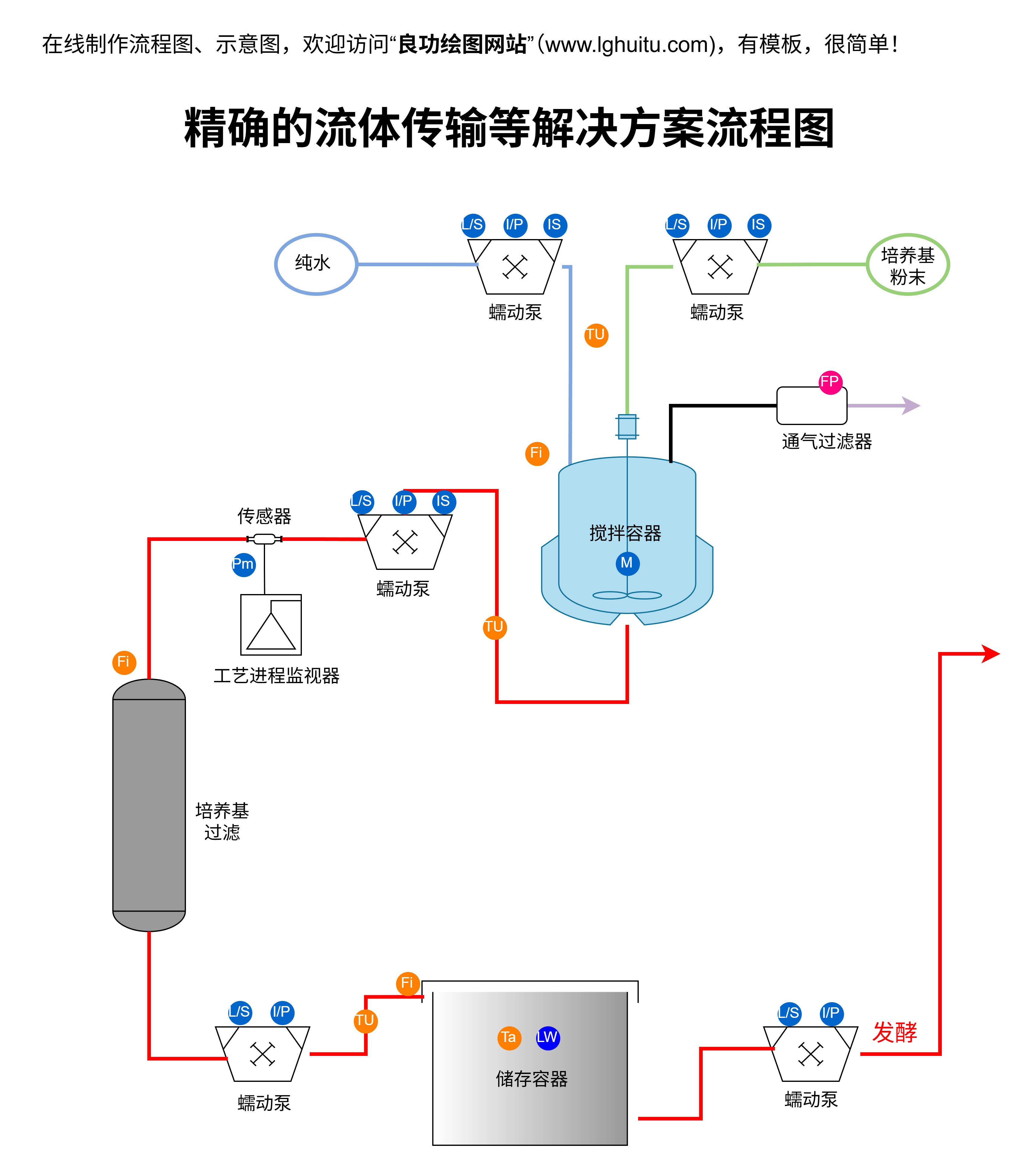
\Deltap=\frac{4fLQ^2}{\pi^2D^5}
其中,(\Deltap)是压差,f是摩擦因子,L是管道长度,Q是流量,D是管道直径。通过这一方程,我们可以看出,流量Q的增加会使压差△p显著增大。特别是在长管道和小直径管道中,这一效应尤为显著。
理解Q与△p之间的关系,对实际工程项目具有重要的指导意义。例如,在油气管道的设计中,工程师需要计算合适的流量和压差,以保证管道输送效率并避免过大的能量损失。过高的压差会导致泵的负担增加,能源消耗过大,甚至可能引发设备故障。
流量和压差的关系在空气调节、供水系统以及化工生产中同样具有重要应用。在风机和泵的选择中,往往需要根据流体的特性来计算合适的流量和压差,以确保系统的运行稳定和高效。
流量Q和压差△p之间的关系不仅受管道长度和直径的影响,还受到多种因素的制约。例如,流体的粘度、密度、流态(层流或湍流)等都直接影响着这一关系。
流体粘度:流体的粘度是衡量流体内部分子之间相互摩擦力的程度。在流体流动时,较高的粘度会增加管道内的摩擦力,进而导致更高的压差。因此,高粘度流体的流量较小,而低粘度流体则容易通过管道。
流态的变化:流体在管道中可能呈现层流或湍流状态。层流通常出现在低流速条件下,流体的流动平稳且可预测。而湍流则是高速流动时的常见现象,流动不规则,压力损失较大。在湍流状态下,压差和流量之间的关系更加复杂。
管道内壁的光滑程度:管道的内壁越光滑,流体流动时的摩擦力就越小,压差也相对较小。而粗糙的管道内壁会增加流体的摩擦,导致更大的压差。
在流体力学的实际应用中,优化Q和△p之间的关系可以提高系统的效率,降低能量损失。比如,在设计一条石油管道时,工程师可以通过选择适当的管道直径、调整流速、改进泵和风机的配置,来降低不必要的压差,确保系统的运行效率最大化。
现代的计算流体力学(CFD)技术为优化设计提供了强大的工具。通过计算机模拟,工程师可以在设计阶段预测流量和压差的变化,及时发现潜在问题,从而采取有效的解决方案。这种技术的广泛应用,大大提高了工程设计的精准性和经济性。
Q和△p之间的关系是流体力学中的核心原理之一,其影响遍及各个工程领域。从简单的水管输送到复杂的工业系统,这一关系都对系统的设计和运行效率产生深远影响。掌握流量和压差之间的关系,不仅能帮助我们理解流体流动的基本原理,还能在实际应用中优化系统性能,降低能耗,提高生产效率。在未来的工程应用中,随着科技的不断进步,流体力学的理论和技术将持续推动各个行业的革新与发展。