在小学数学的世界里,奥数不仅仅是高难度的数学题目集合,它更多的是一种思维的培养和能力的提升。而在奥数的众多领域中,几何题目无疑是最具挑战性的之一。几何问题不仅需要孩子们掌握一定的几何基础知识,还需要他们拥有灵活的空间想象能力和逻辑推理能力。
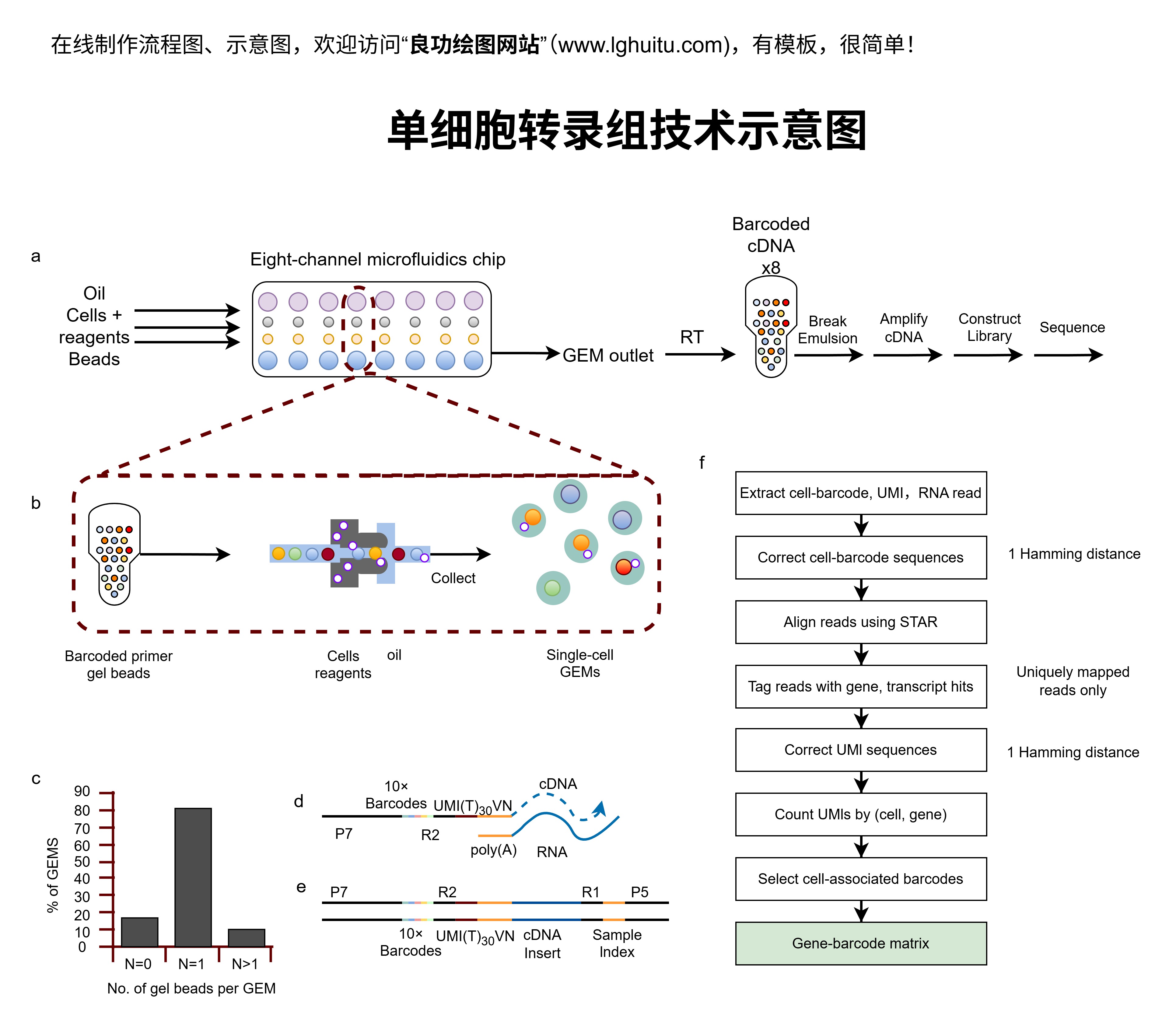
几何模型作为小学奥数中的重要组成部分,通过图形、空间的描绘与转换,帮助孩子们理解几何题目背后的规律和技巧。这些模型不仅使学生能够轻松解决实际问题,还能激发他们的创造力和解决复杂问题的能力。让我们一起探索几何模型在小学奥数中的应用和重要性。
几何模型是通过图形、线条、角度等几何元素的组合来帮助学生理解和解决几何问题的一种方法。它通过简化复杂的几何结构,让孩子们更容易把抽象的几何概念转化为具体的图形,帮助他们理解和记忆解题思路。例如,平面几何模型常用来解答关于三角形、四边形、圆等形状的基本性质问题;而立体几何模型则主要用于解决与立方体、圆柱体、球体等立体形状相关的问题。
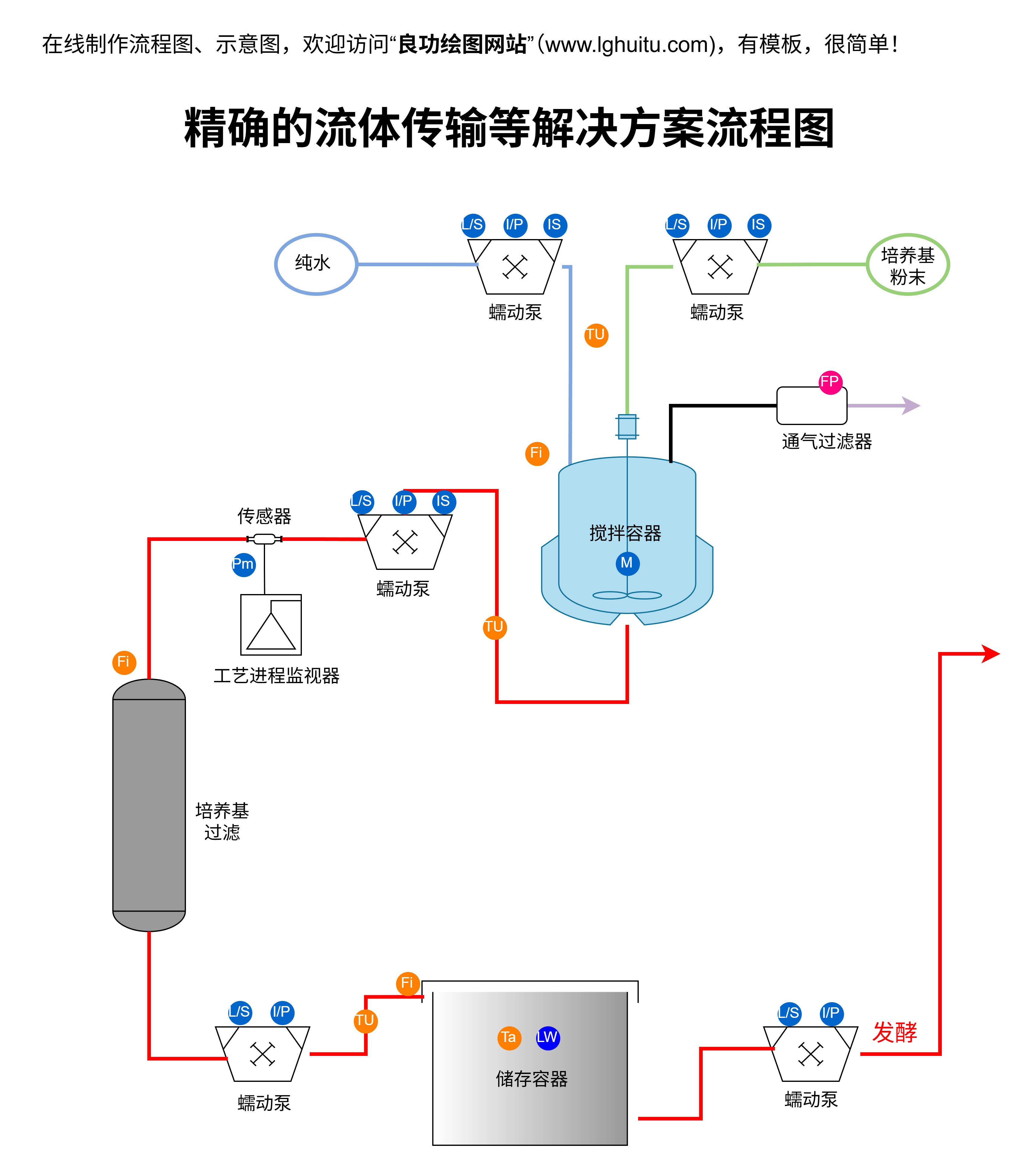
空间想象力是小学生在解答几何题目时所需要的重要能力之一。通过几何模型的帮助,学生能够更加直观地理解不同几何形状的属性及其相互关系。举个例子,当孩子们学习到平面上的角度计算时,他们通过绘制几何图形来找出角度的大小,从而避免了单纯依赖公式计算的枯燥。
例如,在学习如何计算一个多边形的内角和时,学生可以通过画出具体的几何模型,看到多个三角形拼接而成的形状,从而得出一个多边形的内角和公式。这种方式不仅提高了学生的理解深度,还增强了他们的几何思维能力。
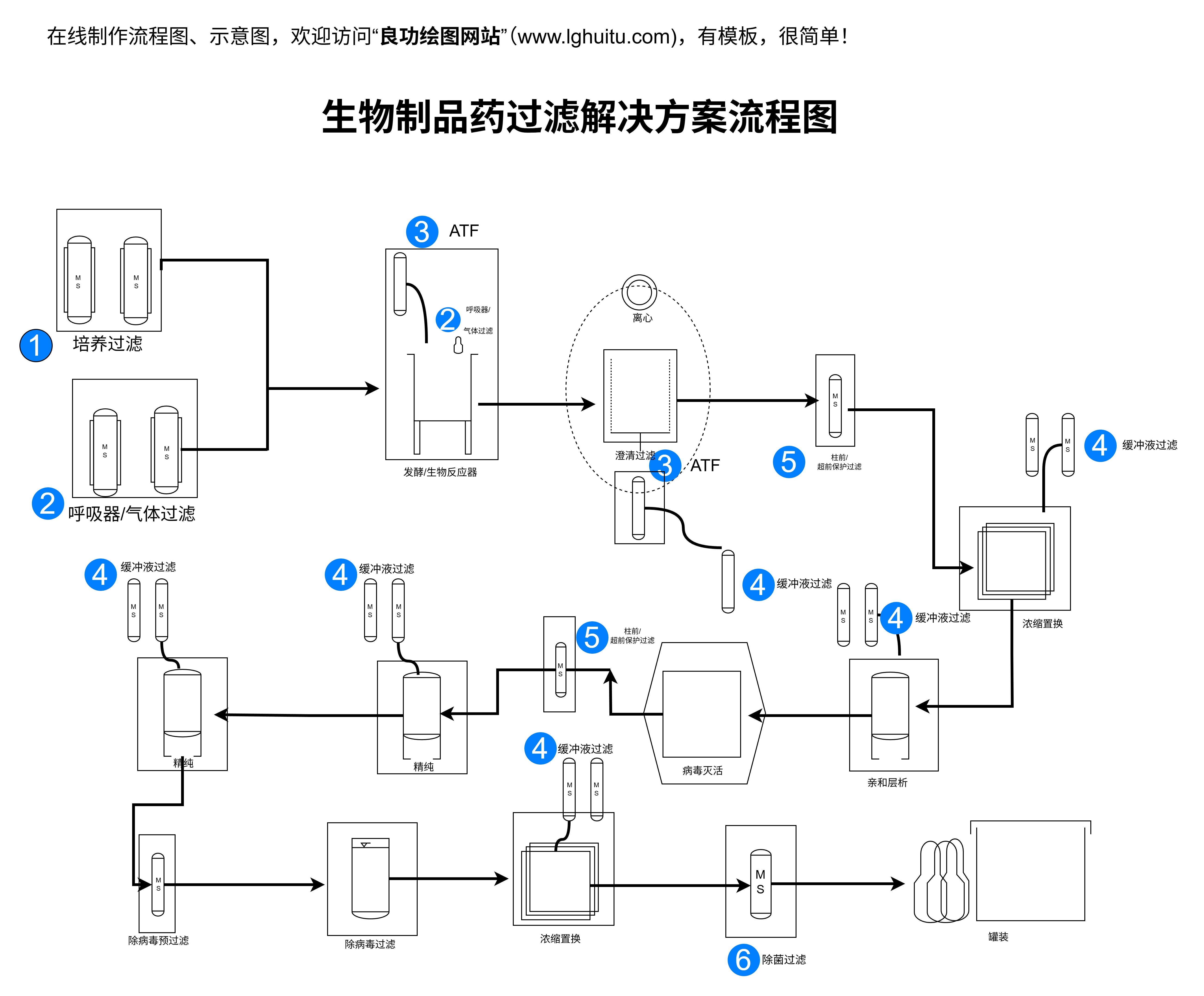
奥数作为一种数学竞赛,其目的是通过具有挑战性的数学题目激发学生的思维潜力。在几何题型中,学生经常会遇到需要应用几何模型的情况。例如,关于圆的几何题目,学生可能需要运用圆的切线、弧长等概念,而这时几何模型就可以帮助他们直观地理解这些抽象的概念。
立体几何题目则往往需要学生将三维的空间结构转化为平面图形,通过几何模型的构建,学生能够更好地理解立体图形的性质,从而轻松解答相关题目。
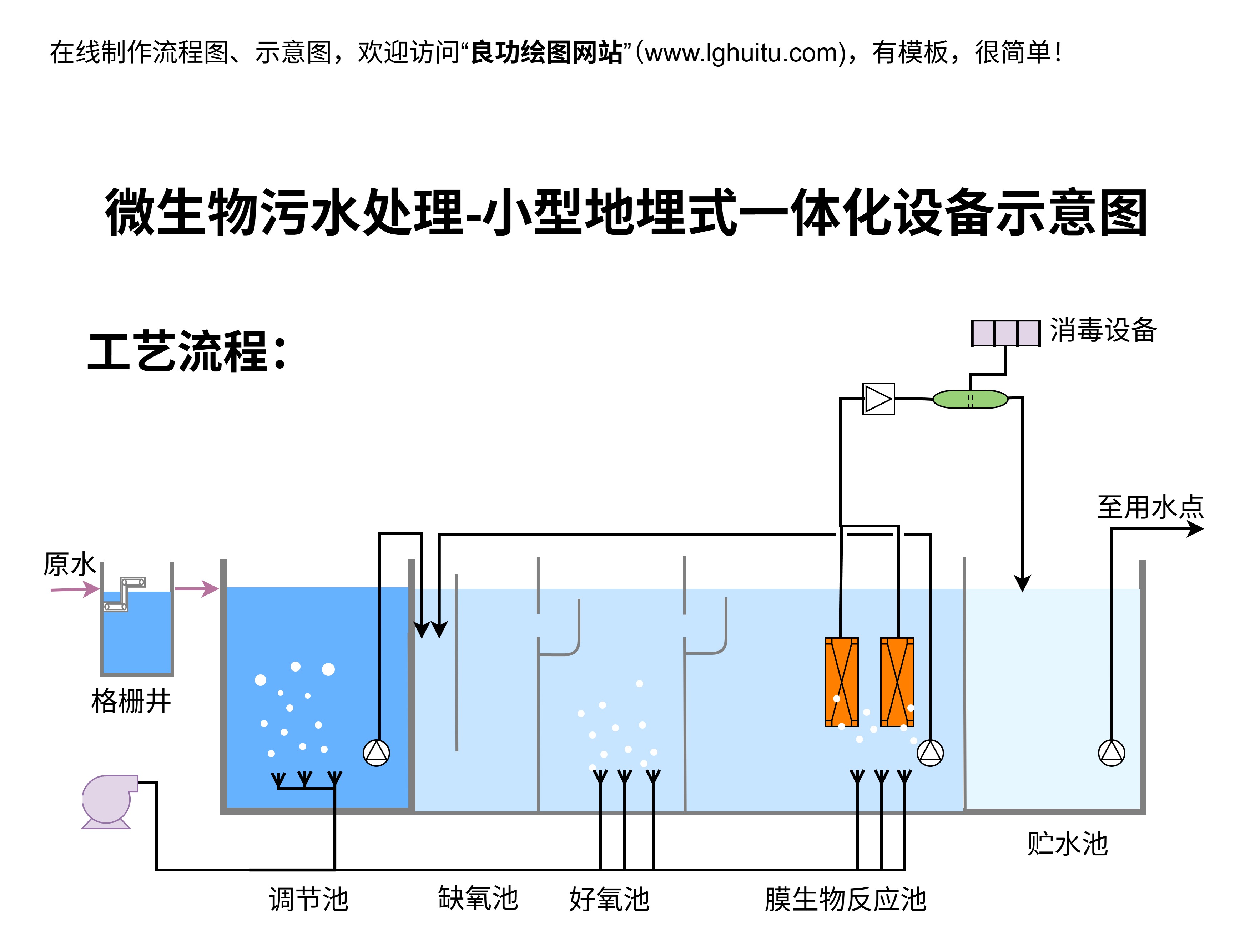
几何模型在小学奥数中有着丰富的种类。每种模型都有其独特的特点和应用场景,以下是一些常见的几何模型及其特点:
平面几何模型:这类模型主要是二维图形的组合与变换,常用于解决关于角度、面积、周长、对称性等问题。平面几何模型中的三角形、矩形、正方形、圆等形状是基础,学生通过这些基础图形的变换和组合,能够理解复杂几何图形的构造与性质。
立体几何模型:这类模型涉及到三维空间中的几何体,如立方体、长方体、圆柱体、球体等。学生通过学习这些立体几何模型,能够更好地理解三维空间的概念,并将其转化为平面图形进行分析。例如,学生通过展开立方体模型来理解其表面积的计算方法。
几何变换模型:这类模型通过旋转、平移、反射等几何变换帮助学生理解图形之间的关系。例如,通过平移一个三角形,学生可以发现其形状和大小不变,而位置发生了变化,这有助于培养学生对几何变换的理解。
投影与剖面模型:这种模型帮助学生理解如何将三维物体转化为二维图形进行分析。通过剖面图,学生可以清晰地看到立体图形的内部结构,并推理出其各种性质。尤其在解决空间几何问题时,投影与剖面模型起到了至关重要的作用。
要掌握几何模型的应用,学生不仅需要了解各类几何图形的性质,还需要培养一定的数学思维方式。以下是一些有效的学习方法:
动手绘制几何图形:学生可以通过动手绘制几何图形,逐步建立起几何形状与其性质之间的联系。动手实践可以帮助学生更直观地理解抽象的几何概念,同时培养他们的空间想象力。
利用软件辅助学习:随着科技的发展,许多几何学习软件应运而生。这些软件通过虚拟图形的展示,帮助学生更好地理解几何模型的变化和转化。学生可以通过旋转、缩放图形等方式,全面了解几何形状的性质。
做大量的奥数题目:学习几何模型的最好方法就是通过实际的奥数题目进行训练。在解答各种几何问题时,学生可以不断应用不同的几何模型,培养自己的解题技巧和数学思维。
小学奥数中的几何模型不仅是解题工具,更是培养学生数学思维和空间想象力的宝贵资源。通过不断探索和学习几何模型,孩子们不仅能够轻松应对各种几何题目,还能够在更高年级的数学学习中如鱼得水。因此,家长和老师应该重视几何模型的教学,并鼓励孩子们通过动手实践、做题、利用工具等多种方式,提升他们的几何思维能力。
在未来的数学学习中,几何模型将继续发挥重要作用,帮助学生打下扎实的数学基础,开启更加广阔的数学世界。