流体力学是研究流体(液体和气体)运动规律的科学,它在多个领域中发挥着至关重要的作用。从航空航天到汽车工程,再到建筑和水利工程,流体力学的理论和计算方法都直接影响到设计和优化过程。对于工程师和科学家而言,流体的流量计算尤为重要,而qv(体积流量)就是其中的核心计算之一。
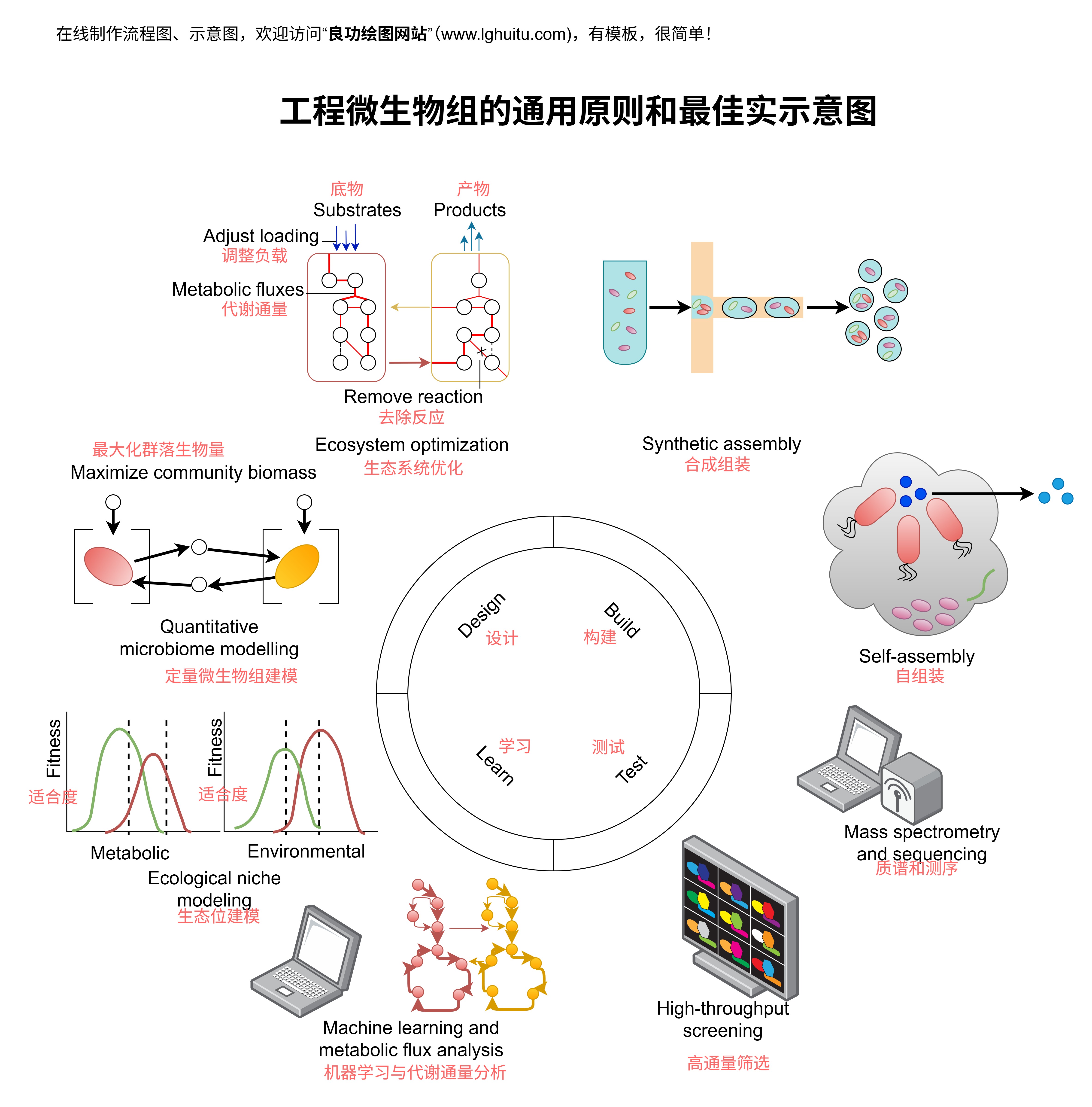
在流体力学中,qv指的是单位时间内通过某一截面的流体体积。它通常用符号qv表示,单位为立方米每秒(m³/s)。了解qv的计算方法,不仅可以帮助我们解决流体流动的基础问题,还能为更复杂的流体力学问题提供支持。
其中,A代表流体通过的截面积,v代表流体的平均流速。这个公式告诉我们,流体的体积流量等于流体通过截面的速度与截面积的乘积。
对于不同类型的流体流动,截面积A可能会有所不同。在管道流动中,A通常是管道的横截面积。而在其他类型的流动,如河流或空气流动,A则可能是流经区域的宽度和高度的乘积。
在管道设计中,qv的计算至关重要。管道的流量直接影响到供水、供气以及排水系统的效率和安全性。在水处理厂或供水系统中,准确测量和控制qv不仅可以确保系统的高效运行,还可以防止由于流量不均导致的管道破裂或泄漏问题。
在航空航天领域,qv用于计算气流在飞机表面的流量,这对飞机的设计至关重要。特别是在计算飞机机翼、尾翼的气动性能时,流量的大小直接影响到升力、阻力等重要参数。
在环保和水资源管理领域,qv被用来测量河流、湖泊或水库的流量。这对于防洪、灌溉等活动至关重要。在水资源紧缺的地区,准确的流量计算帮助科学管理水资源,确保水的合理利用。
虽然qv的计算公式相对简单,但实际计算中常常需要考虑多个因素。流体的性质(如密度、粘度等)、流动状态(如层流与湍流)以及外部条件(如温度、压力等)都会影响流体的流动情况,从而影响qv的计算结果。
例如,气体和液体的密度差异会导致流动特性不同。液体的密度通常较高,流动时不易压缩,而气体的密度较低,流动时容易发生压缩效应。因此,计算气体的体积流量时,需要考虑气体的压缩因子。
流动状态也是影响qv计算的重要因素。在层流状态下,流体的流动较为平稳,流速相对较低;而在湍流状态下,流体的流动不规则,流速较高,且会受到更多外界因素的干扰。因此,在湍流状态下,qv的计算往往需要更复杂的模型来进行修正。
尽管qv的计算公式简单,但在复杂的工程应用中,准确计算流体的体积流量仍然是一个巨大的挑战。在很多实际场景中,流体的流动情况远比理论模型所能描述的要复杂得多。例如,在大规模工业设备或运输系统中,流体的流动可能受到多种因素的影响,如管道的弯曲、流动的非均匀性、外部温度变化等。这些因素需要在qv计算中加以考虑,才能确保计算结果的准确性。
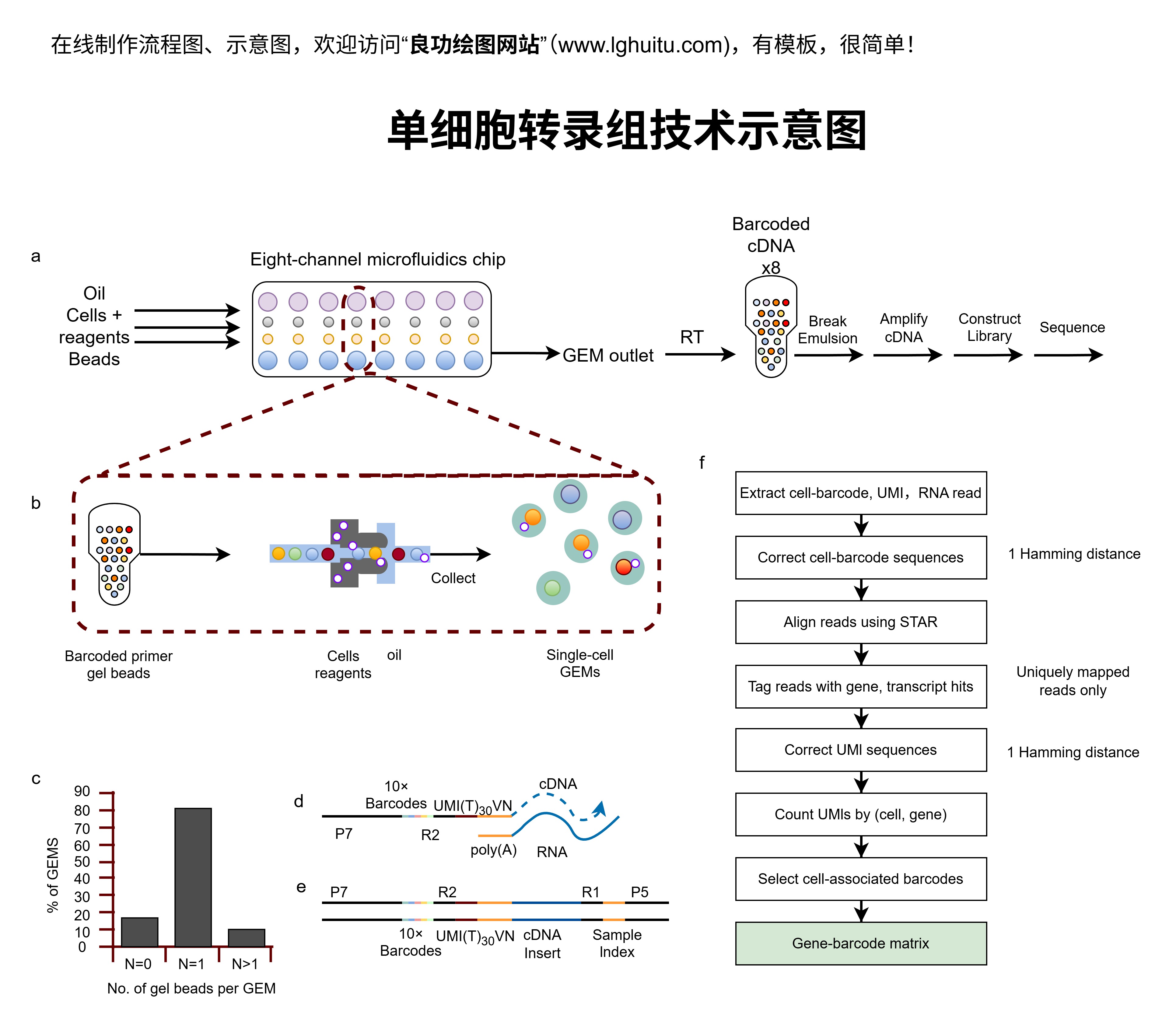
为了提高qv计算的准确性,工程师和研究人员通常会采用更加精细的计算方法和工具。随着计算机技术的进步,数值模拟和CFD(计算流体力学)技术已经成为流体力学计算中的重要手段。CFD能够对流体的流动进行三维建模,并考虑更多的影响因素,从而提供更为精确的流量计算结果。
在工程中,尤其是在复杂流动情况下,传统的解析解往往难以适用。这时,数值模拟成为了一种解决方案。通过CFD仿真,可以模拟流体在不同条件下的行为,进而获得准确的qv值。CFD软件能够处理更复杂的几何形状和流动情况,通过精确的网格划分和流动求解方法,帮助工程师获得更为详细的流量信息。
在气体流动的场景中,温度和压力的变化对qv的影响不可忽视。气体的密度通常随温度和压力的变化而发生显著变化,因此需要通过理想气体状态方程或其他更复杂的状态方程来修正qv的计算结果。
在很多实际应用中,流体的流动并不是恒定不变的,而是具有周期性或非周期性的变化。例如,在某些工业过程中,流体的流速和流量可能随时间波动。为了更加准确地计算qv,工程师需要使用瞬时流量测量技术,并结合流动的时变特性进行动态模拟。
尽管理论计算能够提供流量的初步估算,但在许多实际应用中,通过仪器进行现场测量得到的流量数据才是最为可靠的。常用的流量计,如电磁流量计、涡街流量计等,能够实时测量流体的流量,并为qv计算提供实际依据。将测量数据与理论计算相结合,可以有效提高流量计算的精度。
随着科学技术的不断发展,qv的计算方法和技术也在不断进步。现代流体力学不仅仅局限于传统的工程应用,新的技术和应用领域也在不断拓展。
在新能源领域,如风力发电和太阳能发电,qv计算帮助我们评估风力和气流的情况,从而提高能量转化效率。例如,通过对风力的体积流量进行精确计算,能够帮助优化风力发电机的设计,最大化风能的利用率。
在生物医学中,qv的计算也有着重要的应用。例如,在研究血流动力学时,通过计算血流的体积流量,可以帮助医生判断血管的健康状况,以及制定治疗方案。同样,在人工心脏的设计中,准确的qv计算对于心脏泵血功能的模拟至关重要。
流体力学中的qv计算不仅仅是一个简单的数学公式,它背后蕴含着丰富的理论和复杂的实践应用。无论是在传统的工业设计,还是在现代的新能源、环保和生物医学领域,qv的计算都发挥着举足轻重的作用。随着技术的不断发展和计算方法的不断改进,流体力学的应用前景更加广阔。掌握qv计算,将为您在流体力学领域的探索提供强大的支持,帮助您应对未来的各种挑战。