流体力学作为一门研究流体(液体与气体)在不同条件下运动规律的科学,在现代工业、航天、气象等众多领域中扮演着至关重要的角色。从飞行器的气动设计到汽车的空气动力学优化,再到气象预测与水资源管理,流体力学的研究成果无处不在。而在这庞大的学科体系中,三大基本方程是流体力学的核心,它们分别是欧拉方程、纳维-斯托克斯方程和伯努利方程。
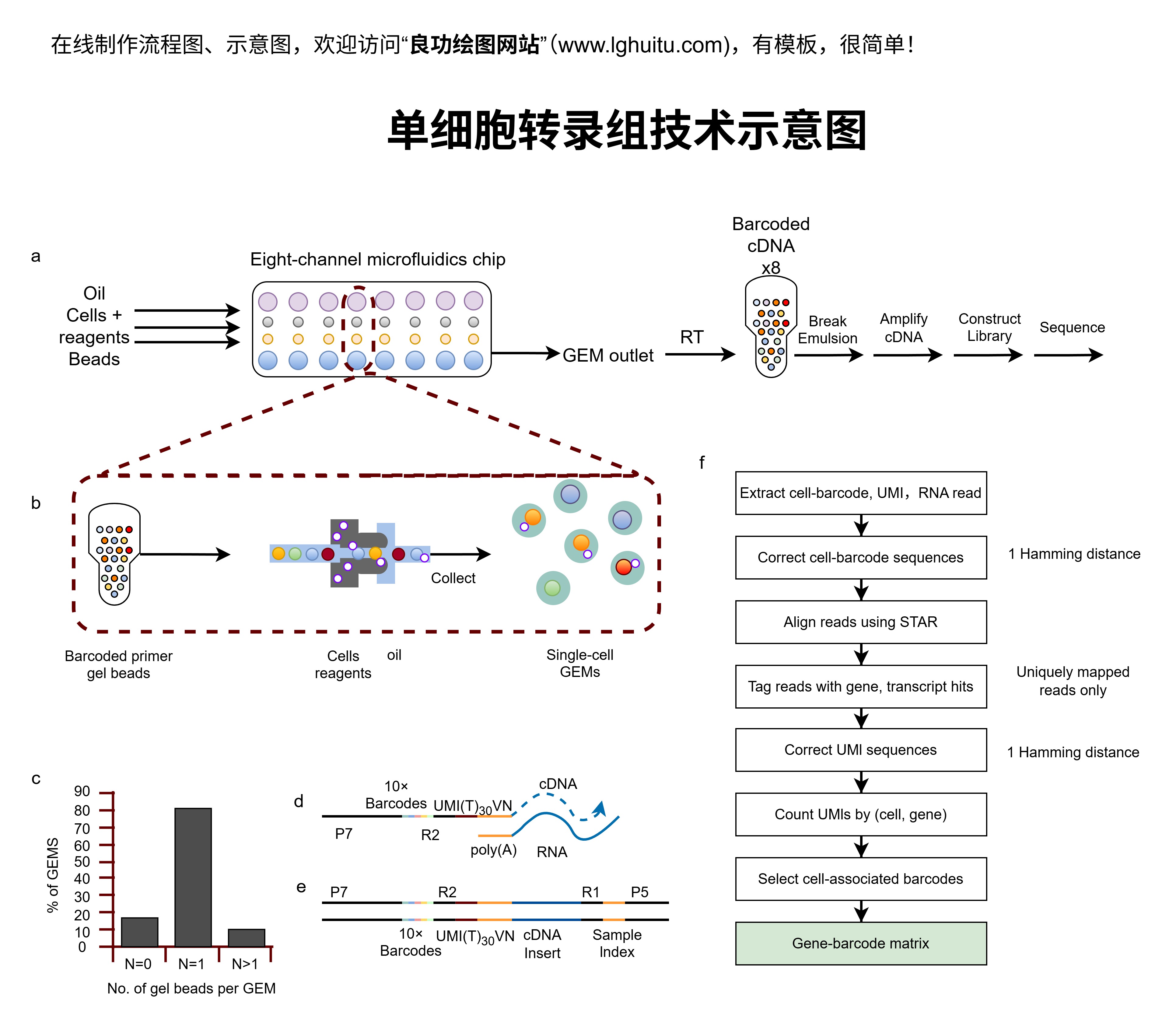
我们来聊聊欧拉方程。欧拉方程是流体力学中描述理想流体(即没有黏性的流体)运动的基本方程之一。它由瑞士数学家欧拉(LeonhardEuler)在18世纪提出,主要用于研究不可压缩流体在流动过程中的速度分布和压力变化。欧拉方程是一组偏微分方程,它揭示了流体在不同位置的速度、压力与密度之间的关系。欧拉方程的提出,使得我们能够通过数学模型来预测理想流体在各种流动状态下的行为,从而为后来的航空航天、气象学等领域的发展奠定了基础。
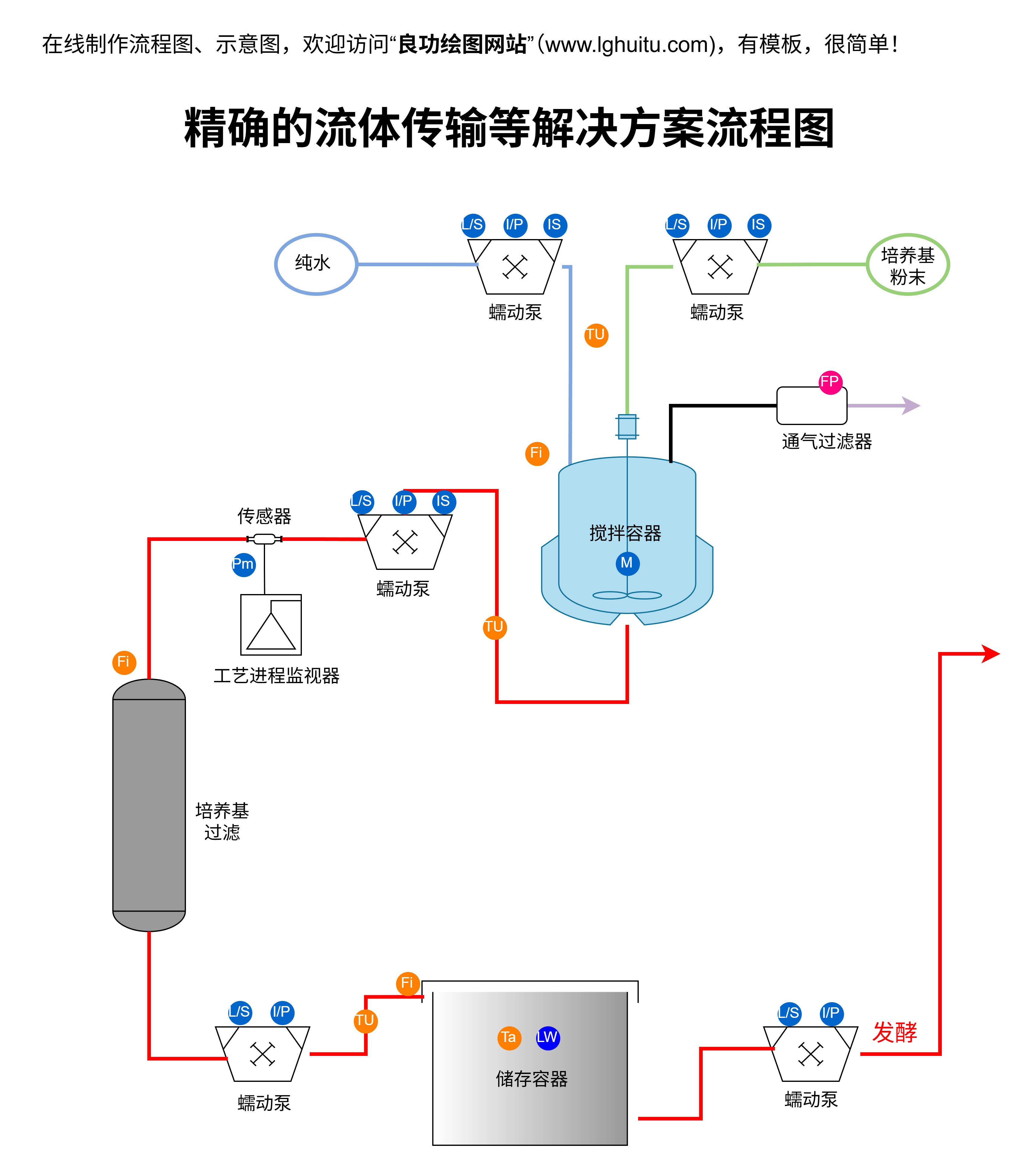
而纳维-斯托克斯方程则是描述实际流体运动的更为复杂的方程。与理想流体不同,实际流体具有黏性,且往往呈现出不可压缩或可压缩的流动特性。纳维-斯托克斯方程正是用来描述这种黏性流体在流动过程中的力学行为。纳维和斯托克斯分别在19世纪提出了这组方程,它们通过描述流体的质量守恒、动量守恒和能量守恒,帮助我们理解了黏性流体在流动过程中如何受到外部力(如重力、压力、摩擦力等)的影响。纳维-斯托克斯方程不仅在理论研究中占据着重要地位,而且在工程实践中也有着广泛的应用。例如,利用这组方程,我们可以模拟天气的变化、研究油气输送管道的流动特性、以及优化航空器和船舶的设计等。
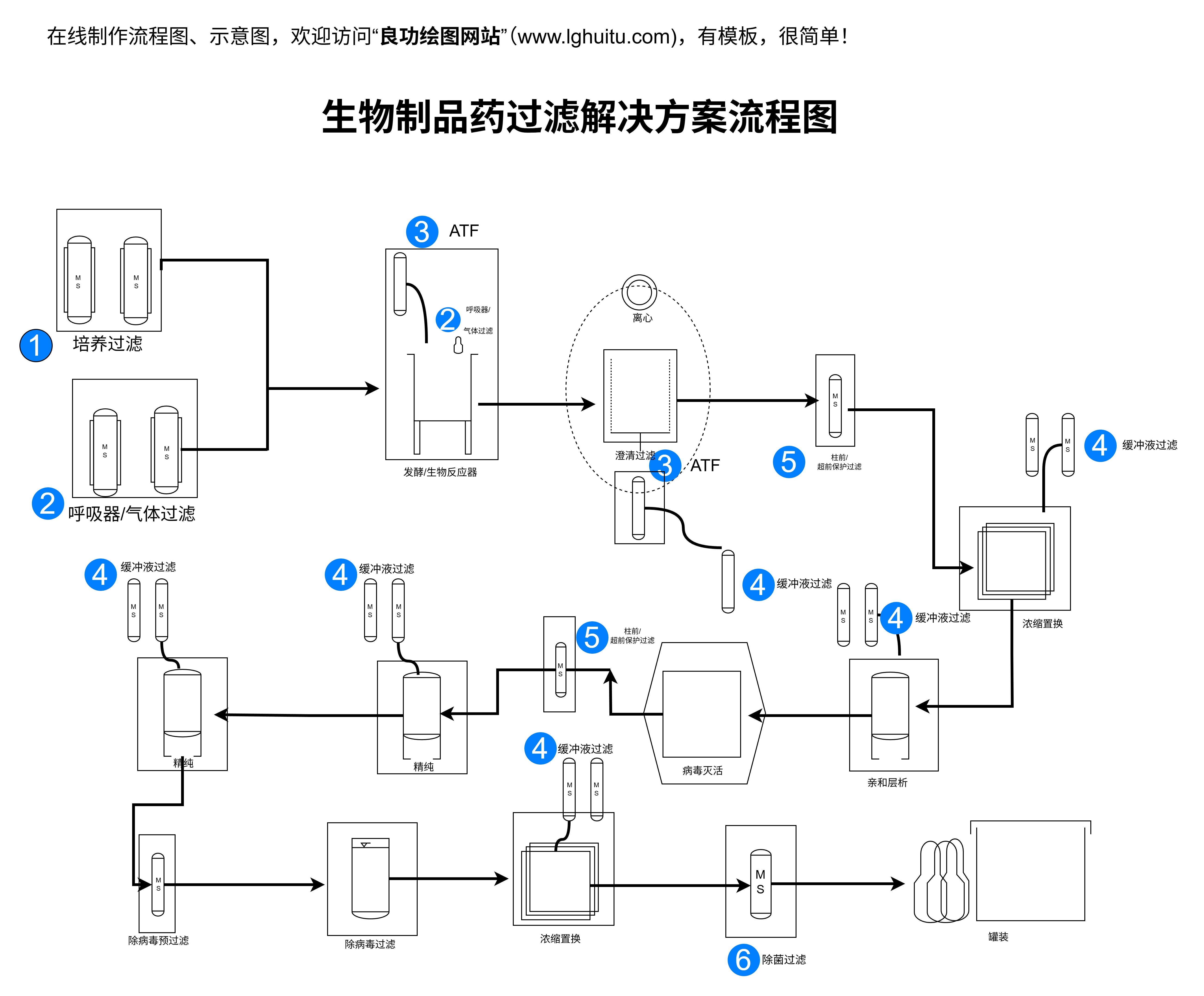
再来看看伯努利方程。伯努利方程是流体力学中的一个经典方程,它是由瑞士工程师伯努利(DanielBernoulli)在18世纪提出的,主要用来描述理想流体的能量守恒原理。伯努利方程简洁而深刻,体现了流体动力学中的能量转化规律。根据伯努利方程,流体的动能、压力能和势能之和在稳态流动中是恒定的。这一理论不仅对航空航天领域中的机翼设计、气流控制等方面有重要影响,而且对各种流体动力学系统的分析与设计也具有指导意义。例如,在飞机的翼型设计中,伯努利方程帮助我们理解机翼上方气流速度加快,气压降低的现象,从而使飞机产生升力。
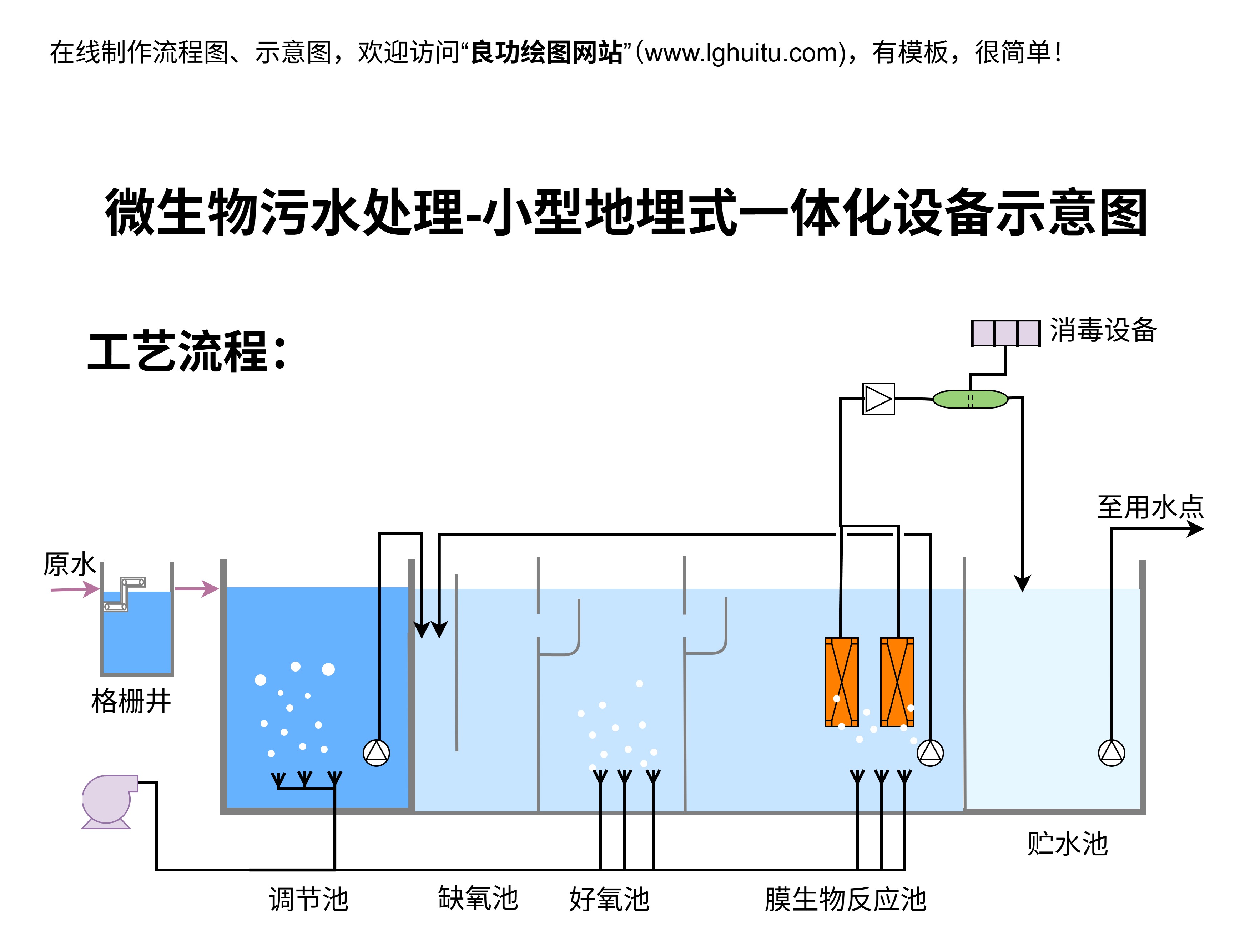
这三大基本方程在流体力学中的地位至关重要,它们不仅为我们提供了深入理解流体行为的理论工具,更推动了科技的进步。无论是在航空航天、海洋工程、环境保护,还是在日常的能源利用、交通运输中,流体力学的应用都无处不在。这些方程在实际生活中如何应用?它们是如何推动我们不断突破技术边界的呢?
流体力学三大基本方程的应用无疑是多样且广泛的。从日常生活中的液体流动到航天航空的气动设计,甚至我们平时使用的管道、风扇和空调等设备,都离不开流体力学的基本理论。让我们从几个实际应用来深入了解这些方程如何助力科技创新。
航天领域的气动设计离不开流体力学的支撑。飞机和火箭的飞行性能都需要经过精密的流体力学计算。尤其是伯努利方程,它帮助设计师理解机翼的升力机制。根据伯努利方程,飞机翼上气流速度的增加导致机翼上方压力的降低,从而使飞机产生升力。航空航天工程师通过对流体的精确模拟和计算,能够设计出更加高效、安全的飞行器,并通过改进空气动力学减少飞行中的阻力,提高燃油效率。
在气象学中,流体力学的三大基本方程也发挥着巨大的作用。天气系统的形成和变化是由大气中的气流、温度变化、湿度等因素引起的,这些因素与流体力学有着密不可分的关系。通过应用欧拉方程、纳维-斯托克斯方程以及伯努利方程,气象学家能够模拟和预测风暴、台风等极端天气现象的形成过程。尤其是纳维-斯托克斯方程,它能帮助研究人员分析大气中复杂的流动模式,从而实现天气的精准预测。
再者,流体力学在工业生产中的应用也是不可忽视的。例如,在石油、天然气的开采和运输过程中,流体力学的基本方程帮助工程师设计高效的输油管道,确保流体在管道中的稳定流动,避免因流动不均匀引起的能量浪费。纳维-斯托克斯方程在这一过程中尤为重要,它能精准描述油气在管道中的流动状态,优化输送效率。
流体力学还广泛应用于环境工程领域。比如,河流的水流管理、水库的水流控制等问题,都需要用到流体力学的基本方程来进行分析。通过对流体力学方程的求解,工程师可以设计出更加科学的水利工程方案,从而有效地解决水资源分配、洪水防治等问题。
流体力学三大基本方程不仅在理论上具有深刻的科学意义,更在实际应用中扮演着无可替代的角色。随着科技的不断进步,流体力学将继续推动航空航天、气象预测、环境保护等领域的发展,引领我们迈向更加高效、智能的未来。而对于每一个从事工程设计、科学研究和技术创新的专业人士来说,掌握流体力学的基本方程,无疑是开拓新技术、实现梦想的关键一步。