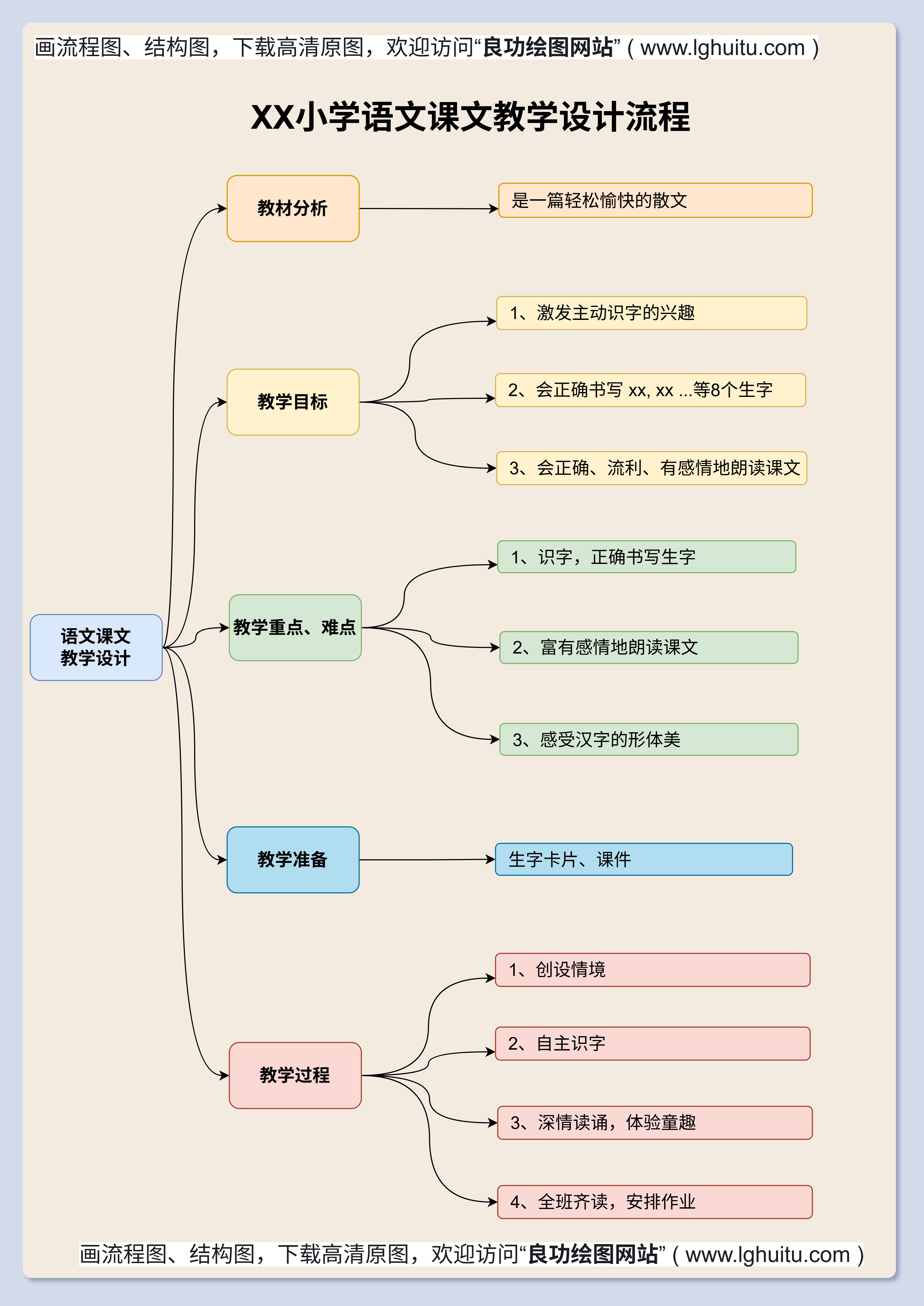
在我们的日常生活中,常常会遇到“比”和“比例”这两个概念。从做菜的调味比例到工程的设计比率,这些看似简单的数字关系,实际上背后蕴藏着非常深奥的数学原理。掌握“比”和“比例”的核心知识,将有助于我们更好地应对这些问题,而思维导图则是一种帮助我们理解和掌握这些概念的高效工具。
“比”是两个数之间关系的表现,通常表示为“a:b”的形式,其中a和b是两个数值。比表示了a与b之间的相对大小关系。例如,如果我们有两个数5和3,5:3就表示了这两个数之间的关系。简单来说,比就是描述两者数量关系的方式,它帮助我们理解一个数值相对于另一个数值的大小。
在生活中,我们经常用比来表达“多少倍”、“几分之一”等概念。例如,当我们说一个篮球队的得分是另一个篮球队的2倍时,这就是一种比的运用。
比例是比的扩展,它表示两个比值相等。我们可以用等式的形式表示比例,例如:a:b=c:d。比例是数学中重要的概念,尤其在解决比例问题时非常有用。比例的基本性质之一是交叉相乘,即:a/b=c/d,可以得到a*d=b*c,这个公式在实际应用中非常广泛。

比例的应用场景非常多,例如在地图上,比例尺就是一个典型的比例应用。比如,1:1000的比例尺表示地图上的1厘米代表现实中的1000厘米,帮助我们在有限的空间里准确表达大范围的地理信息。
在学习过程中,理解比与比例的关系不仅能帮助我们解决具体的数学问题,还能提高我们的逻辑思维能力。比与比例涉及到数学中的分数、百分数、比例、百分比等知识点,掌握这些知识,我们可以更好地理解和解决许多实际问题。
例如,解题时我们常常会遇到比例的应用,像是“解方程”类的问题。掌握比和比例,不仅能帮助我们在考试中获得更高的分数,也能在实际生活中做出更精确的决策。
思维导图作为一种高效的学习工具,能够帮助我们清晰地梳理比与比例的知识结构。在学习比与比例时,使用思维导图能够让我们直观地看到概念之间的联系,并帮助我们建立更加系统的知识框架。
通过思维导图,我们可以将比与比例的相关知识进行有序的整理,从基本概念、公式到实际应用,层层推进,循序渐进。思维导图的结构化和可视化特点,使得复杂的数学概念变得更加易于理解和记忆。
例如,在一个比与比例的思维导图中,我们可以将比和比例的定义、性质、应用等分支分别列出,并在每个分支下详细列出相关的公式、例子和应用场景。通过这样的方式,我们可以轻松地理解和掌握比与比例这一重要的数学工具。
提高理解能力:通过图形化的展示,思维导图能帮助学习者更快速地理解比与比例的概念。视觉化的信息比纯文字更容易被大脑接受,从而提高学习效率。
帮助记忆:思维导图将比与比例的知识按逻辑结构进行分类,减少了死记硬背的负担,使得学习者能够通过图形化的方式轻松记住关键知识点。
增强逻辑思维:在制作思维导图的过程中,学习者需要对比与比例的知识进行梳理和分类,这有助于锻炼逻辑思维能力,并能够更好地将理论与实践相结合。
促进自主学习:思维导图是一种非常适合自主学习的工具。学习者可以根据自己的学习进度和需要,灵活地调整和补充思维导图的内容,逐步提高自己的数学能力。
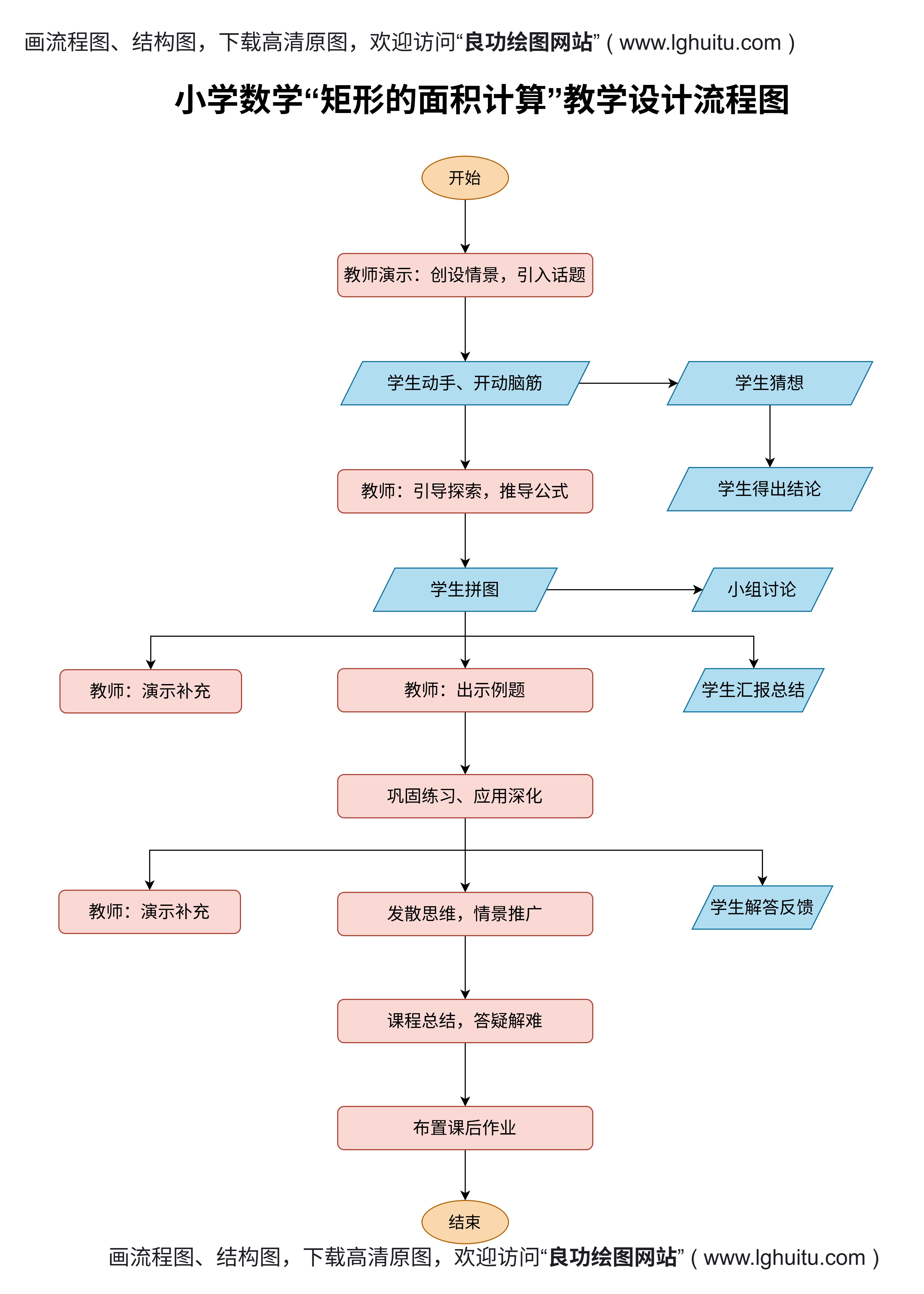
当我们认识到比与比例在数学学习中的重要性后,如何利用思维导图这一工具高效地学习这些内容就成了关键。在本部分中,我们将详细介绍如何构建比与比例的思维导图,并分享一些使用思维导图学习的技巧。
确定核心主题:在创建思维导图时,首先要明确核心主题。在比与比例的学习中,我们的核心主题就是“比与比例”,这一主题应放置在思维导图的中心位置。
划分主要分支:围绕“比与比例”这一主题,我们可以划分出多个主要分支。例如,基本概念、性质、应用、常见问题等。每一个分支代表了比与比例知识的不同方面。
细化分支内容:在每一个主要分支下,我们需要进一步细化内容。例如,在“基本概念”分支下,我们可以列出比和比例的定义、公式、性质等;在“应用”分支下,我们可以列举日常生活中比与比例的应用场景,如地图比例尺、调味比例等。

增加例题与练习:在思维导图中加入相关的例题和练习,帮助我们更好地理解和巩固比与比例的知识。例如,针对比例问题,可以列出一些实际的解题步骤和示例,帮助我们掌握解题技巧。
定期回顾:思维导图不仅是一种知识整理工具,它也是一种复习工具。学习比与比例时,我们可以定期回顾自己制作的思维导图,帮助加深对知识的记忆和理解。
灵活调整:随着学习的深入,我们对比与比例的理解可能会有所变化。此时,我们可以根据需要对思维导图进行调整和优化,增加新的知识点或删除不必要的内容。
结合实际问题:在学习比与比例时,尽量结合实际生活中的问题进行练习。例如,可以根据实际生活中的调味比例来练习比例计算,或通过工程设计中的比例关系来加深对比例概念的理解。
合作学习:思维导图也可以作为小组学习的工具。在小组学习中,大家可以一起讨论和制作思维导图,互相补充知识,共同解决疑难问题。
思维导图不仅适用于比与比例的学习,它还可以应用于数学的其他领域以及其他学科的学习。例如,在几何学、代数学、物理学等领域,思维导图都能够帮助我们清晰地梳理和理解知识点,提升学习效率。
通过结合比与比例的思维导图学习方法,我们可以更高效、更深入地理解这些重要的数学概念。在学习的过程中,思维导图不仅帮助我们整理知识,还能够提高我们的记忆力和逻辑思维能力。无论是在课堂学习还是日常生活中,掌握比与比例的应用,将为我们提供强大的数学支持,帮助我们在各个领域做出更加精准的决策和判断。